|
|
| (5 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
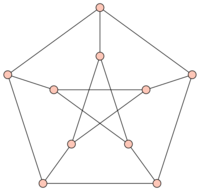
| | A [[Graph|graph]] that has fascinated graph theorists over the years because of its appearance as a counterexample in so many areas of the subject: | | A [[Graph|graph]] that has fascinated graph theorists over the years because of its appearance as a counterexample in so many areas of the subject: |
| | | | |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p120110a.gif" />
| + | [[File:Petersen graph.svg|center|200px]] |
| | | | |
| − | Figure: p120110a
| + | The Petersen graph is cubic, $3$-connected and has $10$ vertices and $15$ edges. There are exactly $19$ connected cubic graphs on $10$ vertices. The number of elements in the set $C ( n )$ of connected cubic graphs on $n$ vertices grows rapidly with $n$; for example, $| C ( 20 ) | = 510489$, $| C ( 30 ) | = 845480228069$. The Petersen graph is the only graph in $C ( 10 )$ with $120$ automorphisms (cf. also [[Graph automorphism|Graph automorphism]]); the only graph in $C ( 10 )$ with girth $5$; the only graph in $C ( 10 )$ with diameter $2$; the only bridgeless graph in $C ( 10 )$ with chromatic index $4$ (cf. also [[Graph colouring|Graph colouring]]) and, finally, it is the only bridgeless non-Hamiltonian graph in $C( 10 )$. |
| | | | |
| − | The Petersen graph is cubic, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201101.png" />-connected and has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201102.png" /> vertices and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201103.png" /> edges. There are exactly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201104.png" /> connected cubic graphs on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201105.png" /> vertices. The number of elements in the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201106.png" /> of connected cubic graphs on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201107.png" /> vertices grows rapidly with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201108.png" />; for example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p1201109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011010.png" />. The Petersen graph is the only graph in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011011.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011012.png" /> automorphisms (cf. also [[Graph automorphism|Graph automorphism]]); the only graph in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011013.png" /> with girth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011014.png" />; the only graph in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011015.png" /> with diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011016.png" />; the only bridgeless graph in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011017.png" /> with chromatic index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011018.png" /> (cf. also [[Graph colouring|Graph colouring]]) and, finally, it is the only bridgeless non-Hamiltonian graph in C<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011019.png" />.
| + | Typically, however, the importance of the Petersen graph is the way it features as the exceptional graph. It is at least arguable that the development of graph theory was in large extent due to the interest in the [[Four-colour problem|four-colour problem]]. P.G. Tait [[#References|[a2]]] showed that every planar graph is $4$-face colourable if and only if every bridgeless cubic planar graph is $3$-edge colourable, that is, if its chromatic index is at most $3$. W.T. Tutte [[#References|[a3]]] conjectured that if $G$ is a bridgeless cubic graph with chromatic index at least $4$, then $G$ is subcontractible to the Petersen graph. Thus, even with the proof of the four-colour theorem there is much to prove beyond the theorem [[#References|[a4]]] and typically the Petersen graph features prominently. In the same vein, W.T. Tutte [[#References|[a3]]] conjectured that if $G$ is a bridgeless graph which does not support a nowhere-zero $4$-flow, then $G$ is subcontractible to the Petersen graph: the four-colour theorem guarantees that every bridgeless planar graph supports a nowhere-zero $4$-flow. Let $\overset{\rightharpoonup}{ G }$ be any orientation of the edges $E ( G )$ of $G$. A nowhere-zero $4$-flow on a graph $G$ is a mapping $f : E ( \vec { G } ) \rightarrow \mathbf{Z} _ { 4 } ^ { * }$ such that at each vertex $v$, $\sum f ( \overset{\rightharpoonup } { e } ) = 0$, where the summation is over all oriented edges $\overset{\rightharpoonup} { e }$ incident with $v$. |
| | | | |
| − | Typically, however, the importance of the Petersen graph is the way it features as the exceptional graph. It is at least arguable that the development of graph theory was in large extent due to the interest in the [[Four-colour problem|four-colour problem]]. P.G. Tait [[#References|[a2]]] showed that every planar graph is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011020.png" />-face colourable if and only if every bridgeless cubic planar graph is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011021.png" />-edge colourable, that is, if its chromatic index is at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011022.png" />. W.T. Tutte [[#References|[a3]]] conjectured that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011023.png" /> is a bridgeless cubic graph with chromatic index at least <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011024.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011025.png" /> is subcontractible to the Petersen graph. Thus, even with the proof of the four-colour theorem there is much to prove beyond the theorem [[#References|[a4]]] and typically the Petersen graph features prominently. In the same vein, W.T. Tutte [[#References|[a3]]] conjectured that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011026.png" /> is a bridgeless graph which does not support a nowhere-zero <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011027.png" />-flow, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011028.png" /> is subcontractible to the Petersen graph: the four-colour theorem guarantees that every bridgeless planar graph supports a nowhere-zero <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011029.png" />-flow. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011030.png" /> be any orientation of the edges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011032.png" />. A nowhere-zero <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011034.png" />-flow on a graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011035.png" /> is a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011036.png" /> such that at each vertex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011038.png" />, where the summation is over all oriented edges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011039.png" /> incident with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p120/p120110/p12011040.png" />.
| + | ====References==== |
| | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. Holton, J. Sheehan, "The Petersen graph" ''Austral. Math. Soc. Lecture Ser., CLT'' , '''7''' (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P.G. Tait, "Remarks on the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1878-80) pp. 729</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.T. Tutte, "On the algebraic theory of graph colourings" ''J. Combin. Th.'' , '''1''' (1966) pp. 15–50</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> W.T. Tutte, "Colouring problems" ''Math. Intelligencer'' , '''1''' (1978) pp. 72–75</td></tr></table> |
| | | | |
| − | ====References====
| + | [[Category:Graph theory]] |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Holton, J. Sheehan, "The Petersen graph" ''Austral. Math. Soc. Lecture Ser., CLT'' , '''7''' (1993)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.G. Tait, "Remarks on the colouring of maps" ''Proc. R. Soc. Edinburgh'' , '''10''' (1878-80) pp. 729</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W.T. Tutte, "On the algebraic theory of graph colourings" ''J. Combin. Th.'' , '''1''' (1966) pp. 15–50</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W.T. Tutte, "Colouring problems" ''Math. Intelligencer'' , '''1''' (1978) pp. 72–75</TD></TR></table>
| |
A graph that has fascinated graph theorists over the years because of its appearance as a counterexample in so many areas of the subject:
The Petersen graph is cubic, $3$-connected and has $10$ vertices and $15$ edges. There are exactly $19$ connected cubic graphs on $10$ vertices. The number of elements in the set $C ( n )$ of connected cubic graphs on $n$ vertices grows rapidly with $n$; for example, $| C ( 20 ) | = 510489$, $| C ( 30 ) | = 845480228069$. The Petersen graph is the only graph in $C ( 10 )$ with $120$ automorphisms (cf. also Graph automorphism); the only graph in $C ( 10 )$ with girth $5$; the only graph in $C ( 10 )$ with diameter $2$; the only bridgeless graph in $C ( 10 )$ with chromatic index $4$ (cf. also Graph colouring) and, finally, it is the only bridgeless non-Hamiltonian graph in $C( 10 )$.
Typically, however, the importance of the Petersen graph is the way it features as the exceptional graph. It is at least arguable that the development of graph theory was in large extent due to the interest in the four-colour problem. P.G. Tait [a2] showed that every planar graph is $4$-face colourable if and only if every bridgeless cubic planar graph is $3$-edge colourable, that is, if its chromatic index is at most $3$. W.T. Tutte [a3] conjectured that if $G$ is a bridgeless cubic graph with chromatic index at least $4$, then $G$ is subcontractible to the Petersen graph. Thus, even with the proof of the four-colour theorem there is much to prove beyond the theorem [a4] and typically the Petersen graph features prominently. In the same vein, W.T. Tutte [a3] conjectured that if $G$ is a bridgeless graph which does not support a nowhere-zero $4$-flow, then $G$ is subcontractible to the Petersen graph: the four-colour theorem guarantees that every bridgeless planar graph supports a nowhere-zero $4$-flow. Let $\overset{\rightharpoonup}{ G }$ be any orientation of the edges $E ( G )$ of $G$. A nowhere-zero $4$-flow on a graph $G$ is a mapping $f : E ( \vec { G } ) \rightarrow \mathbf{Z} _ { 4 } ^ { * }$ such that at each vertex $v$, $\sum f ( \overset{\rightharpoonup } { e } ) = 0$, where the summation is over all oriented edges $\overset{\rightharpoonup} { e }$ incident with $v$.
References
| [a1] | D. Holton, J. Sheehan, "The Petersen graph" Austral. Math. Soc. Lecture Ser., CLT , 7 (1993) |
| [a2] | P.G. Tait, "Remarks on the colouring of maps" Proc. R. Soc. Edinburgh , 10 (1878-80) pp. 729 |
| [a3] | W.T. Tutte, "On the algebraic theory of graph colourings" J. Combin. Th. , 1 (1966) pp. 15–50 |
| [a4] | W.T. Tutte, "Colouring problems" Math. Intelligencer , 1 (1978) pp. 72–75 |