Obstacle scattering
Let 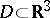 be a bounded domain with boundary
be a bounded domain with boundary 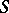 . A large amount of literature, going back to the mid-1930s, deals with wave scattering by obstacles when
. A large amount of literature, going back to the mid-1930s, deals with wave scattering by obstacles when 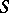 is smooth, for example, a
is smooth, for example, a 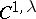 -surface,
-surface, 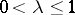 . (See [a3], [a17], [a2].)
. (See [a3], [a17], [a2].)
The obstacle scattering problem consists of finding the solution to the equation
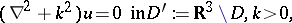 | (a1) |
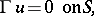 | (a2) |
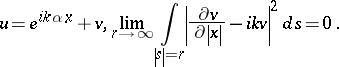 | (a3) |
Here 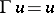 ( the Dirichlet condition), or
( the Dirichlet condition), or 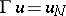 (the Neumann condition) or
(the Neumann condition) or 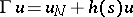 (the Robin condition), where
(the Robin condition), where 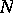 is the unit normal to
is the unit normal to 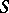 pointing into
pointing into 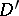 and
and 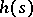 is a continuous function (cf. also Dirichlet boundary conditions; Neumann boundary conditions). Condition (a3) is the radiation condition, which selects a unique solution to problem (a1)–(a3). In (a3),
is a continuous function (cf. also Dirichlet boundary conditions; Neumann boundary conditions). Condition (a3) is the radiation condition, which selects a unique solution to problem (a1)–(a3). In (a3), 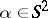 is a given unit vector, the direction of the incident plane wave
is a given unit vector, the direction of the incident plane wave 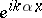 , and
, and 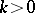 is the wave number.
is the wave number.
The scattering problem (a1)–(a3) has a solution and the solution is unique. This basic result was proved originally by the integral equations method [a3].
There are many different types of integral equations which allow one to study problem (a1)–(a3) (see [a17], where most of these equations are derived).
The scattering field  in (a3) has the following asymptotics:
in (a3) has the following asymptotics:
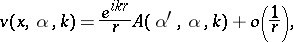 | (a4) |
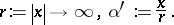 |
The function 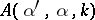 is called the scattering amplitude. This function has the following properties [a17]:
is called the scattering amplitude. This function has the following properties [a17]:
i) realness: 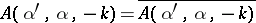 ,
, 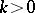 , the bar stands for complex conjugation;
, the bar stands for complex conjugation;
ii) reciprocity:  ;
;
iii) unitarity:
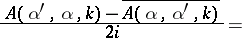 |
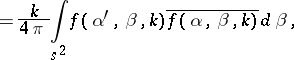 |
and its consequence, which is called the optical theorem:
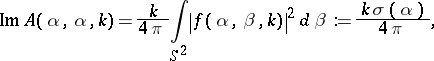 |
where 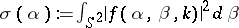 is called the cross-section.
is called the cross-section.
The function  is analytic with respect to
is analytic with respect to 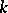 in
in 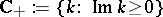 and meromorphic in
and meromorphic in 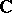 ; it is analytic with respect to
; it is analytic with respect to 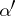 and
and 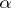 on the variety
on the variety 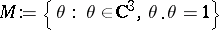 , where
, where  , see [a17], [a18] (cf. also Analytic function; Meromorphic function).
, see [a17], [a18] (cf. also Analytic function; Meromorphic function).
Necessary and sufficient conditions for a scatterer to be spherically symmetric is: 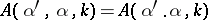 , where
, where 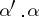 is the dot product [a18], [a8].
is the dot product [a18], [a8].
The solution 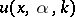 to (a1)–(a3) is called the scattering solution. Any
to (a1)–(a3) is called the scattering solution. Any 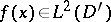 can be expanded with respect to scattering solutions:
can be expanded with respect to scattering solutions:
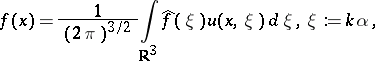 |
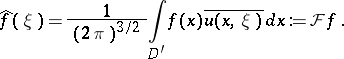 |
The operator 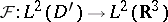 is unitary:
is unitary: 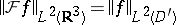 ,
, 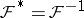 , see [a17] (cf. also Unitary operator).
, see [a17] (cf. also Unitary operator).
The above results hold in 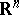 with odd
with odd  . In
. In 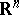 with even
with even  the scattering amplitude
the scattering amplitude 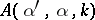 as a function of complex
as a function of complex 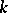 has a logarithmic branch point at
has a logarithmic branch point at 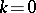 .
.
The scattering problem with minimal assumptions on the smoothness of the boundary 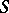 is studied in [a13]. If
is studied in [a13]. If 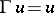 , then existence and uniqueness of the scattering solution have been proved without any assumption on the smoothness of the boundary
, then existence and uniqueness of the scattering solution have been proved without any assumption on the smoothness of the boundary  of a bounded domain
of a bounded domain 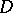 . In this case a weak formulation of problem (a1)–(a3) is considered and the limit-absorption principle has been proved.
. In this case a weak formulation of problem (a1)–(a3) is considered and the limit-absorption principle has been proved.
If 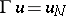 , then again a weak formulation of (a1)–(a3) is considered and the only assumption on the smoothness of the boundary
, then again a weak formulation of (a1)–(a3) is considered and the only assumption on the smoothness of the boundary 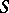 is compactness of the embedding
is compactness of the embedding 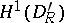 into
into 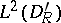 , where
, where 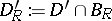 and
and 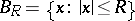 is a ball which contains
is a ball which contains 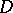 . Existence and uniqueness of the scattering solution have been proved and the limiting-absorption principle has been established. Finally, if
. Existence and uniqueness of the scattering solution have been proved and the limiting-absorption principle has been established. Finally, if 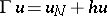 , then the same results are obtained under the assumptions of compactness of the embeddings
, then the same results are obtained under the assumptions of compactness of the embeddings 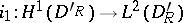 and
and 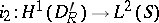 , where
, where 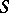 is equipped with the
is equipped with the 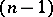 -dimensional Hausdorff measure and
-dimensional Hausdorff measure and 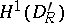 is the Sobolev space.
is the Sobolev space.
For example, the embedding 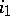 is compact for C-domains, that is, domains whose boundary can be covered by finitely many sets open in
is compact for C-domains, that is, domains whose boundary can be covered by finitely many sets open in  and on each of these sets the equation of
and on each of these sets the equation of 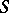 in a local coordinate system can be written as
in a local coordinate system can be written as 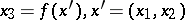 , where
, where 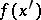 is a continuous function.
is a continuous function.
The scattering problem for one obstacle, small in comparison with the wavelength (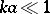 , where
, where  is the diameter of the small obstacle), for many such bodies (the number
is the diameter of the small obstacle), for many such bodies (the number 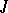 of bodies of order
of bodies of order 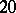 ), and in a medium consisting of many such bodies randomly distributed in the space, has been studied in [a7] and later in [a16]. Formulas for the scattering amplitude for acoustic and electromagnetic wave scattering by small bodies of arbitrary shapes are derived in [a16].
), and in a medium consisting of many such bodies randomly distributed in the space, has been studied in [a7] and later in [a16]. Formulas for the scattering amplitude for acoustic and electromagnetic wave scattering by small bodies of arbitrary shapes are derived in [a16].
These formulas for acoustic wave scattering on a single small body, containing the origin, are
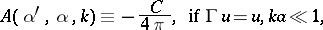 |
where 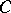 is the electrical capacitance of the body
is the electrical capacitance of the body 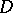 ;
;
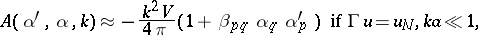 |
where over the repeated indices one sums up from 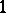 to
to  ,
,  is the volume of
is the volume of 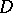 and
and 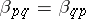 is the magnetic polarizability tensor;
is the magnetic polarizability tensor;
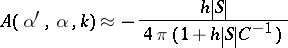 |
 |
where  is the area of the boundary
is the area of the boundary 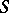 .
.
The  -matrix for electromagnetic wave scattering by a small homogeneous body of arbitrary shape is:
-matrix for electromagnetic wave scattering by a small homogeneous body of arbitrary shape is:
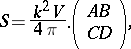 |
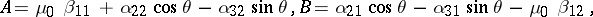 |
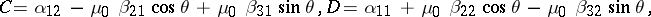 |
where 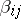 and
and 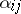 are tensors of magnetic and electric polarizability and
are tensors of magnetic and electric polarizability and 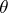 is the angle between the direction
is the angle between the direction 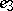 of the incident field and the direction of the scattered field;
of the incident field and the direction of the scattered field; 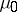 is the magnetic permeability of the medium in which the small body is embedded (cf. also Scattering matrix).
is the magnetic permeability of the medium in which the small body is embedded (cf. also Scattering matrix).
Formulas for the tensors  and
and 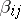 are derived in [a7] and [a16].
are derived in [a7] and [a16].
One can derive an equation for the average field in the medium which consists of many small obstacles (particles) randomly distributed in a region. This done in [a16] and [a6].
Scattering by random surfaces is studied in [a1].
Inverse obstacle scattering.
Three inverse obstacle scattering problems are of interest:
ISP1) Given 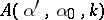 for all
for all 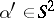 and all
and all 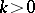 ,
, 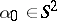 being fixed, find
being fixed, find 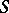 and the boundary condition on
and the boundary condition on 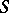 .
.
ISP2) Given 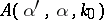 for all
for all 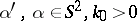 being fixed, find
being fixed, find 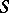 and the boundary condition on
and the boundary condition on 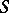 .
.
ISP3) Given 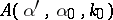 for all
for all 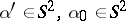 and
and  being fixed, find
being fixed, find 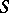 .
.
Uniqueness of the solution to ISP1) (for 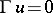 ) was first proved by M. Schiffer (1964), whose argument is given in [a17].
) was first proved by M. Schiffer (1964), whose argument is given in [a17].
Uniqueness of the solution to ISP2) was first proved by A.G. Ramm (1985) and his proof is given in [a17].
A uniqueness theorem for ISP3) has not yet (2000) been proved: it is an open problem to prove (or disprove the existence of) such a theorem.
One can consider inverse obstacle scattering for penetrable obstacles [a14].
Schiffer's proof of the uniqueness theorem is based on a result saying that the spectrum of the Dirichlet Laplacian in any bounded domain is discrete. This result follows from the compactness of the embedding 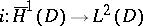 for any bounded domain (without any assumptions on the smoothness of its boundary
for any bounded domain (without any assumptions on the smoothness of its boundary 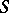 ),
), 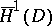 is the Sobolev space which is the closure in
is the Sobolev space which is the closure in 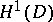 of
of 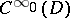 . It is known [a5] that
. It is known [a5] that 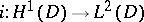 is not compact for rough domains (it is compact for Lipschitz domains, for domains satisfying the cone condition, for C-domains, and for E-domains, i.e. domains for which a bounded extension operator from
is not compact for rough domains (it is compact for Lipschitz domains, for domains satisfying the cone condition, for C-domains, and for E-domains, i.e. domains for which a bounded extension operator from 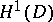 into
into  exists, see [a5]).
exists, see [a5]).
Therefore the spectrum of a Neumann Laplacian in such a rough domain for which the imbedding 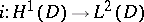 is not compact is not discrete. One way out is given in [a12] and another one in [a11].
is not compact is not discrete. One way out is given in [a12] and another one in [a11].
Suppose that  and
and 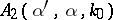 are scattering amplitudes at a fixed
are scattering amplitudes at a fixed 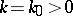 for two obstacles and let
for two obstacles and let 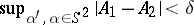 .
.
Assume that the boundaries of the two obstacles are 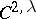 ,
, 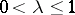 , that is, in local coordinates these boundaries
, that is, in local coordinates these boundaries 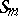 ,
, 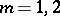 , have equations
, have equations 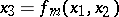 , where
, where 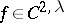 ,
, 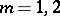 ,
, 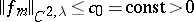 .
.
Let 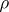 denote the Hausdorff distance between
denote the Hausdorff distance between 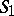 and
and 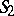 :
: 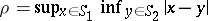 .
.
The basic stability result [a10] is:
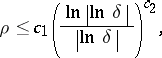 |
where 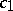 and
and 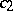 are positive constants.
are positive constants.
In [a10] a yet open problem (as of 2000) is formulated: Derive an inversion formula for finding 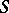 , given the data
, given the data 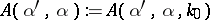 ,
, 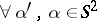 .
.
The existence of such a formula is proved in [a10]: if 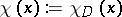 is the characteristic function of
is the characteristic function of 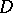 and
and 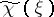 is its Fourier transform, then there exists a function
is its Fourier transform, then there exists a function 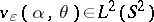 such that
such that
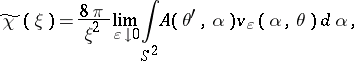 |
where 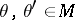 ,
, 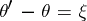 ,
, 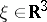 is an arbitrary vector. A formula for calculating
is an arbitrary vector. A formula for calculating 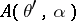 ,
, 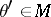 , given
, given 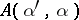 ,
, 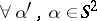 , is derived in [a10]. The problem is to construct
, is derived in [a10]. The problem is to construct 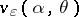 from the data
from the data 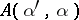 algorithmically. For inverse potential scattering this is done in [a15].
algorithmically. For inverse potential scattering this is done in [a15].
References
| [a1] | F. Bass, I. Fuks, "Wave scattering from statistically rough surfaces" , Pergamon (1979) |
| [a2] | D. Colton, R. Kress, "Integral equations methods in scattering theory" , Wiley (1983) |
| [a3] | V. Kupradze, "Randwertaufgaben der Schwingungstheorie und Integralgleichungen" , DVW (1956) |
| [a4] | R. Leis, "Initial boundary value problems in mathematical physics" , New York (1986) |
| [a5] | V. Maz'ja, "Sobolev spaces" , Springer (1985) |
| [a6] | V. Marchenko, E. Khruslov, "Boundary value problems in domains with granulated boundary" , Nauk. Dumka, Kiev (1974) (In Russian) |
| [a7] | A.G. Ramm, "Theory and applications of some new classes of integral equations" , Springer (1980) |
| [a8] | A.G. Ramm, "Necessary and sufficient condition for a scattering amplitude to correspond to a spherically symmetric scatterer" Appl. Math. Lett. , 2 (1989) pp. 263–265 |
| [a9] | A.G. Ramm, "Stability estimates for obstacle scattering" J. Math. Anal. Appl. , 188 : 3 (1994) pp. 743–751 |
| [a10] | A.G. Ramm, "Stability of the solution to inverse obstacle scattering problem" J. Inverse Ill-Posed Probl. , 2 : 3 (1994) pp. 269–275 |
| [a11] | A.G. Ramm, "New method for proving uniqueness theorems for obstacle inverse scattering problems" Appl. Math. Lett. , 6 : 6 (1993) pp. 19–22 |
| [a12] | A.G. Ramm, "Uniqueness theorems for inverse obstacle scattering problems in Lipschitz domains" Applic. Anal. , 59 (1995) pp. 377–383 |
| [a13] | A.G. Ramm, M. Sammartino, "Existence and uniqueness of the scattering solutions in the exterior of rough domains" A.G. Ramm (ed.) P.N. Shivakumar (ed.) A.V. Strauss (ed.) , Operator Theory and Its Applications , Fields Inst. Commun. , 25 , Amer. Math. Soc. (2000) pp. 457–472 |
| [a14] | A.G. Ramm, P. Pang, G. Yan, "A uniqueness result for the inverse transmission problem" Internat. J. Appl. Math. , 2 : 5 (2000) pp. 625–634 |
| [a15] | A.G. Ramm, "Stability estimates in inverse scattering" Acta Applic. Math. , 28 : 1 (1992) pp. 1–42 |
| [a16] | A.G. Ramm, "Iterative methods for calculating the static fields and wave scattering by small bodies" , Springer (1982) |
| [a17] | A.G. Ramm, "Scattering by obstacles" , Reidel (1986) |
| [a18] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a19] | A.G. Ramm, "Spectral properties of the Schroedinger operator in some domains with infinite boundaries" Soviet Math. Dokl. , 152 (1963) pp. 282–285 |
| [a20] | A.G. Ramm, "Reconstruction of the domain shape from the scattering amplitude" Radiotech. i Electron. , 11 (1965) pp. 2068–2070 |
| [a21] | A.G. Ramm, "Approximate formulas for tensor polarizability and capacitance of bodies of arbitrary shape and its applications" Soviet Phys. Dokl. , 195 (1970) pp. 1303–1306 |
| [a22] | A.G. Ramm, "Electromagnetic wave scattering by small bodies of an arbitrary shape" V. Varadan (ed.) , Acoustic, Electromagnetic and Elastic Scattering: Focus on T-Matrix Approach , Pergamon (1980) pp. 537–546 |
| [a23] | A.G. Ramm, "On inverse diffraction problem" J. Math. Anal. Appl. , 103 (1984) pp. 139–147 |
| [a24] | F. Ursell, "On the exterior problems of acoustics" Proc. Cambridge Philos. Soc. , 74 (1973) pp. 117–125 (See also: 84 (1978), 545-548) |
| [a25] | I. Vekua, "Metaharmonic functions" Trudy Tbil. Math. Inst. , 12 (1943) pp. 105–174 (In Russian) |
Obstacle scattering. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Obstacle_scattering&oldid=18755