O-group
totally ordered group
A 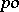 -group
-group 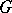 whose partial order is total (cf. also Totally ordered group). A
whose partial order is total (cf. also Totally ordered group). A 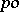 -group is an
-group is an  -group if and only if
-group if and only if 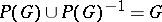 , where
, where 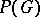 is the positive cone of
is the positive cone of 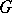 . Every Abelian torsion-free group, every locally nilpotent-torsion free group and every free group can be turned into an
. Every Abelian torsion-free group, every locally nilpotent-torsion free group and every free group can be turned into an  -group. Any
-group. Any  -group
-group 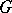 is a quotient group of a free
is a quotient group of a free  -group
-group 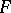 with suitable order by some convex normal subgroup. Direct, Cartesian, free, and direct wreath products of
with suitable order by some convex normal subgroup. Direct, Cartesian, free, and direct wreath products of  -groups can be turned in
-groups can be turned in  -groups by extending the orders of the factors. Any
-groups by extending the orders of the factors. Any  -group is a topological group respect with to the interval topology. Any
-group is a topological group respect with to the interval topology. Any  -group can be imbedded into simple
-group can be imbedded into simple  -groups. There exist non-Hopfian
-groups. There exist non-Hopfian  -groups.
-groups.
If 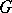 is an
is an  -group, then the group-theoretical structure of
-group, then the group-theoretical structure of 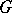 is very nice. In particular, any
is very nice. In particular, any  -group has a subnormal solvable system of subgroups, it is a torsion-free group and a group with unique roots. Thus,
-group has a subnormal solvable system of subgroups, it is a torsion-free group and a group with unique roots. Thus,  -groups are suitable examples in the study of many classes of groups. The system
-groups are suitable examples in the study of many classes of groups. The system  of convex subgroups of an
of convex subgroups of an  -group is well studied (cf. Convex subgroup). In particular,
-group is well studied (cf. Convex subgroup). In particular,  is the central series of isolated normal subgroups for any locally nilpotent
is the central series of isolated normal subgroups for any locally nilpotent  -group.
-group.
It is useful to apply methods from the theory of semi-groups to questions about orderability of a group. Let 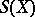 be the normal sub-semi-group of a group
be the normal sub-semi-group of a group 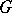 generated by a set
generated by a set 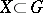 . Then
. Then 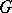 is orderable (i.e., it is possible to turn
is orderable (i.e., it is possible to turn 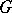 in an
in an  -group) if and only if
-group) if and only if 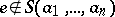 for all
for all  (
(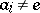 ). Every partial order
). Every partial order  can be extended to a total order on
can be extended to a total order on 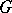 if and only if for all
if and only if for all 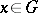 ,
, 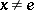 implies
implies 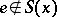 and for all
and for all 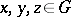 ,
,
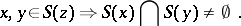 |
Groups with this property are called fully orderable. If a group is torsion-free and Abelian, or locally nilpotent or orderable metabelian, then it is fully orderable. The class of fully orderable groups is closed under formation of direct products and is locally closed. It is not closed under formation of subgroups, Cartesian products, free products. It is non-axiomatizable.
This article complements the article Totally ordered group (Vol. 9).
References
| [a1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [a2] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Halstad (1974) (In Russian) |
| [a3] | R.T.B. Mura, A.H. Rhemtulla, "Orderable groups" , M. Dekker (1977) |
| [a4] | V.M. Kopytov, N.Ya. Medvedev, "The theory of lattice-ordered groups" , Kluwer Acad. Publ. (1994) (In Russian) |
O-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=O-group&oldid=14111