Noether problem
The question of the rationality of the field of invariants of a finite group acting by automorphisms on a field of rational functions. More precisely, let 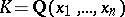 be the field of rational functions in
be the field of rational functions in  variables with coefficients in the field
variables with coefficients in the field  of rational numbers, so that
of rational numbers, so that 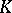 is a purely transcendental extension of
is a purely transcendental extension of 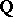 of transcendence degree
of transcendence degree  . Also, let
. Also, let 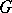 be a finite group acting by automorphisms on
be a finite group acting by automorphisms on  by means of permutations of the variables
by means of permutations of the variables  . The question is now whether the subfield
. The question is now whether the subfield 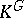 of
of 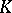 consisting of all elements fixed under
consisting of all elements fixed under  is itself a field of rational functions in
is itself a field of rational functions in  (other) variables with coefficients in
(other) variables with coefficients in 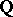 . This question was raised by E. Noether [1] in connection with the inverse problem of Galois theory (cf. Galois theory, inverse problem of). If the answer to Noether's problem were affirmative, one could construct a Galois extension of
. This question was raised by E. Noether [1] in connection with the inverse problem of Galois theory (cf. Galois theory, inverse problem of). If the answer to Noether's problem were affirmative, one could construct a Galois extension of 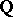 with a given finite group
with a given finite group 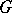 (see [5]). The problem is also closely connected with the Lüroth problem.
(see [5]). The problem is also closely connected with the Lüroth problem.
In general, the answer to Noether's problem is negative. The first example of a non-rational field 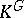 was constructed in [2], and in this example
was constructed in [2], and in this example  is generated by a cyclic permutation of the variables. In [3] it was established that the necessary condition for the rationality of
is generated by a cyclic permutation of the variables. In [3] it was established that the necessary condition for the rationality of 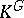 found in [2] is also sufficient. The question of rationality of
found in [2] is also sufficient. The question of rationality of 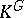 in the case of an Abelian group
in the case of an Abelian group 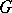 is closely connected with the theory of algebraic tori (cf. Algebraic torus) (see [4]).
is closely connected with the theory of algebraic tori (cf. Algebraic torus) (see [4]).
Frequently, Noether's problem is interpreted more generally as the problem that arises when in the original setting 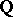 is replaced by an arbitrary field
is replaced by an arbitrary field 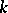 . This problem has an affirmative solution, for example, when
. This problem has an affirmative solution, for example, when 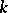 is algebraically closed and
is algebraically closed and 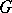 is Abelian.
is Abelian.
References
| [1] | E. Noether, "Gleichungen mit vorgeschriebener Gruppe" Math. Ann. , 78 (1917–1918) pp. 221–229 |
| [2] | R.G. Swan, "Invariant rational functions and a problem of Steenrod" Invent. Math. , 7 : 2 (1969) pp. 148–158 |
| [3] | V.E. Voskresenskii, "Rationality of certain algebraic tori" Math. USSR. Izv. , 35 : 5 (1979) pp. 1049–1056 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 1037–1046 |
| [4] | V.E. Voskresenskii, "Algebraic tori" , Moscow (1977) (In Russian) |
| [5] | N.G. Chebotarev, "Grundzüge der Galois'schen Theorie" , Noordhoff (1950) pp. Chapt. V §4 (Translated from Russian) |
Comments
For  arbitrary and
arbitrary and 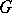 finite Abelian, there is a necessary and sufficient condition for rationality of
finite Abelian, there is a necessary and sufficient condition for rationality of 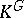 (see [a1]). For example, if
(see [a1]). For example, if 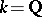 and
and 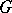 is cyclic of order
is cyclic of order  , then
, then 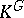 is not rational.
is not rational.
For 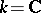 , the first examples of groups
, the first examples of groups 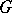 for which
for which 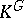 is not rational were constructed by D.J. Saltman [a2]. He proved that for each prime number
is not rational were constructed by D.J. Saltman [a2]. He proved that for each prime number 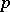 there exists such a group of order
there exists such a group of order 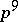 .
.
References
| [a1] | H.W. Lenstra Jr., "Rational functions invariant under a finite abelian group" Invent. Math. , 25 (1974) pp. 299–325 |
| [a2] | D.J. Saltman, "Noether's problem over an algebraically closed field" Invent. Math. , 77 (1984) pp. 71–84 |
Noether problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noether_problem&oldid=11427