Moving-average process

A stochastic process which is stationary in the wide sense and which can be obtained by applying some linear transformation to a process with non-correlated values (that is, to a white noise process). The term is often applied to the more special case of a process 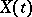in discrete time 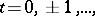that is representable in the form

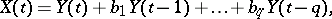(1)

where 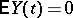, , 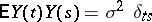with 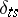the Kronecker delta (so that 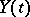is a white noise process with spectral density 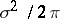), 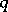is a positive integer, and 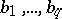are constant coefficients. The spectral density of such a process is given by

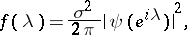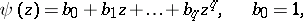and its correlation function 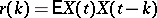has the form

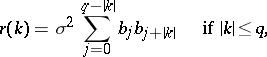Conversely, if the correlation function 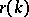of a stationary process 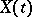in discrete time 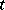has the property that when 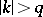for some positive integer 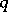, then is a moving-average process of order , that is, it has a representation of the form (1) where is a white noise (see, for example, [1]).

Along with the moving-average process of finite order 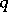, which is representable in the form (1), there are two types of moving-average processes in discrete time of infinite order, namely: one-sided moving-average processes, having a representation of the form

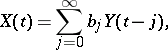(2)

where denotes white noise and the series on the right-hand side converges in mean-square (so that ), and also more general two-sided moving-average processes, of the form

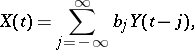(3)

where 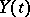denotes white noise and 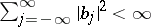. The class of two-sided moving-average processes coincides with that of stationary processes 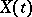having spectral density 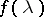, while the class of one-sided moving-average processes coincides with that of processes having spectral density 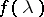such that

(see [2], [1], [3]).

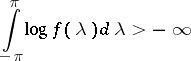A continuous-time stationary process 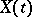, , 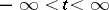is called a one-sided or two-sided moving-average process if it has the form

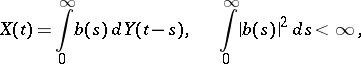or

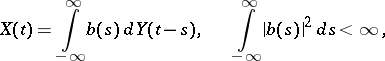respectively, where 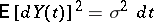, that is, 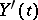is a generalized white noise process. The class of two-sided moving-average processes in continuous time coincides with that of stationary processes 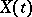having spectral density 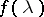, while the class of one-sided moving-average processes in continuous time coincides with that of processes having spectral density 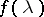such that

(see [4], [3], [5]).

References

[1]	T.M. Anderson, "The statistical analysis of time series" , Wiley (1971)
[2]	A.N. Kolmogorov, "Stationary sequences in Hilbert space" T. Kailath (ed.) , Linear Least-Squares Estimation , Benchmark Papers in Electric Engin. Computer Sci. , 17 , Dowden, Hutchington & Ross (1977) pp. 66–89 (Translated from Russian)
[3]	J.L. Doob, "Stochastic processes" , Wiley (1953)
[4]	K. Karhunun, "Ueber lineare Methoden in der Wahrscheinlichkeitsrechnung" Ann. Acad. Sci. Fennicae Ser. A. Math. Phys. , 37 (1947)
[5]	Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian)

Comments

Both auto-regressive processes (cf. Auto-regressive process) and moving-average processes are special cases of so-called ARMA processes, i.e. auto-regressive moving-average processes (cf. Mixed autoregressive moving-average process), which are of great importance in the study of time series.