Morse lemma
The statement describing the structure of the germ of a twice continuously-differentiable function. Let 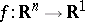 be a function of class
be a function of class 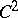 , having the point
, having the point 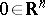 as a non-degenerate critical point. Then in some neighbourhood
as a non-degenerate critical point. Then in some neighbourhood 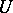 of
of  there is a local coordinate system (a chart)
there is a local coordinate system (a chart)  , with centre at
, with centre at  , so that for all
, so that for all 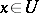 ,
,
 |
Here the number 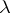 ,
, 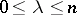 , is the Morse index of the critical point
, is the Morse index of the critical point  of
of 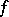 . An analogue of the Morse lemma for functions
. An analogue of the Morse lemma for functions  is also true, namely: If
is also true, namely: If  is holomorphic in a neighbourhood of a non-degenerate critical point (in other terminology, a saddle point, see Saddle point method)
is holomorphic in a neighbourhood of a non-degenerate critical point (in other terminology, a saddle point, see Saddle point method) 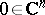 , then in some neighbourhood
, then in some neighbourhood 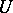 of
of  there is a local coordinate system
there is a local coordinate system  such that
such that
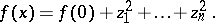 |
The Morse lemma also holds for functions 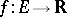 on a separable (infinite-dimensional) Hilbert space
on a separable (infinite-dimensional) Hilbert space 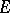 . Let
. Let 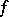 be twice (Fréchet) differentiable in some neighbourhood of a non-degenerate critical point
be twice (Fréchet) differentiable in some neighbourhood of a non-degenerate critical point 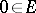 . Then there are a convex neighbourhood of zero
. Then there are a convex neighbourhood of zero 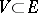 , a convex neighbourhood of zero
, a convex neighbourhood of zero 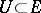 and a diffeomorphism (a chart)
and a diffeomorphism (a chart) 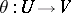 with
with 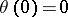 , such that for all
, such that for all 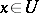 ,
,
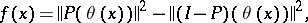 |
where 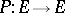 is a continuous orthogonal projection and
is a continuous orthogonal projection and 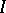 is the identity operator. Here the dimension
is the identity operator. Here the dimension 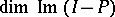 coincides with Morse index of the critical point
coincides with Morse index of the critical point 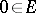 of
of 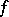 and the dimension
and the dimension 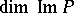 coincides with its co-index.
coincides with its co-index.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) |
Comments
There exist generalizations of the Morse lemma to the following cases:
Equivariant Morse lemma.
Consider a holomorphic function 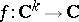 that is invariant with respect to the linear action of a compact subgroup
that is invariant with respect to the linear action of a compact subgroup 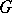 on
on 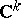 . If
. If  has at
has at  a critical point with critical value
a critical point with critical value  , then it can be reduced to its quadratic part by a
, then it can be reduced to its quadratic part by a 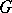 -invariant change of independent variables, biholomorphic at the point
-invariant change of independent variables, biholomorphic at the point  .
.
An analogous "equivariant Morse lemma" is true in the real-analytic and the differentiable context. Cf. [a1] and [a2].
Morse lemma depending on parameters.
Let  be a real-valued differentiable function defined in a neighbourhood of
be a real-valued differentiable function defined in a neighbourhood of 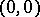 . Let
. Let 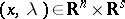 . Assume that
. Assume that 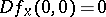 and that
and that 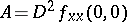 is non-singular. Then there exist coordinates
is non-singular. Then there exist coordinates 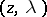 in a neighbourhood of
in a neighbourhood of 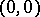 such that
such that
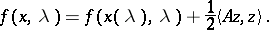 |
In this formula 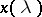 is the local solution of the equations
is the local solution of the equations 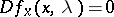 and
and 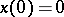 . The proof is a modification of that in the case without parameters. A good reference is [a3], p. 502.
. The proof is a modification of that in the case without parameters. A good reference is [a3], p. 502.
References
| [a1] | V.I. Arnol'd, "Wave front evolution and the equivariant Morse lemma" Comm. Pure Appl. Math. , 29 (1976) pp. 557–582 |
| [a2] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) |
| [a3] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3. Pseudo-differential operators , Springer (1985) |
| [a4] | R.S. Palais, "Morse theory on Hilbert manifolds" Topology , 2 (1963) pp. 299–340 |
Morse lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_lemma&oldid=18472