Lovász local lemma
LLL
A central technique in the probabilistic method. It is used to prove the existence of a "good" object even when the random object is almost certainly "bad" . It is applicable in situations in which the bad events are mostly independent. It sieves the bad events to find the rare good one.
Let 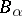 ,
, 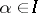 , be a finite family of "bad" events. A graph
, be a finite family of "bad" events. A graph 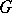 on
on 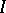 is called a dependency graph for the events if each
is called a dependency graph for the events if each 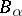 is mutually independent of those
is mutually independent of those 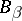 with
with 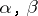 not adjacent (cf. also Independence).
not adjacent (cf. also Independence).
Symmetric case of the Lovász local lemma.
Let 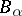 ,
, 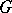 be as above. Suppose all
be as above. Suppose all 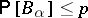 . Suppose all
. Suppose all 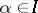 are adjacent to at most
are adjacent to at most 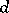 other
other 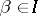 . Suppose
. Suppose 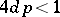 . Then
. Then 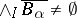 .
.
Here, the number of events, 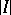 , may be arbitrarily high, giving the Lovász local lemma much of its strength. In most applications the underlying probability space is generated by mutually independent choices, each event
, may be arbitrarily high, giving the Lovász local lemma much of its strength. In most applications the underlying probability space is generated by mutually independent choices, each event 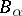 depends on a set
depends on a set 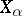 of choices, and
of choices, and 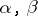 are adjacent when
are adjacent when 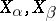 overlap.
overlap.
Example.
Let 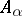 ,
, 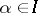 , be sets of size ten in some universe
, be sets of size ten in some universe  , where every
, where every 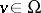 lies in at most ten such sets. Then there is a red-blue colouring of
lies in at most ten such sets. Then there is a red-blue colouring of  so that no
so that no 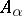 is monochromatic. The underlying space is a random red-blue colouring of
is monochromatic. The underlying space is a random red-blue colouring of  . The bad event
. The bad event 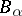 is that
is that 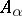 has been coloured monochromatically. Each
has been coloured monochromatically. Each 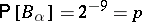 . Each
. Each 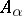 overlaps at most
overlaps at most 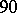 other
other 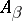 , so
, so 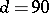 . The Lovász local lemma gives the existence of a colouring.
. The Lovász local lemma gives the existence of a colouring.
The lemma was discovered by L. Lovász (see [a3] for an original application) in 1975. It ushered in a new era for the probabilistic method.
General case of the Lovász local lemma.
Let 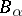 ,
, 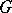 be as above. If there exist an
be as above. If there exist an 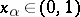 with
with
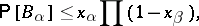 |
the product over those 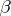 adjacent to
adjacent to 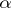 , then
, then 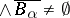 .
.
Application of the general case generally requires mild analytic skill in choosing the 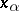 .
.
The proof of the Lovász local lemma (in either case) requires only elementary (albeit ingenious) probability theory and takes less than a page.
A breakthrough in algorithmic implementation was given by J. Beck [a2] in 1991. He showed that in certain (though not all) situations where the Lovász local lemma guarantees the existence of an object, that object can be found by a polynomial-time algorithm. Proofs, applications and algorithmic implementation are explored in [a1] and elsewhere.
The acronym LLL is also used for the Lenstra–Lenstra–Lovász algorithm (see LLL basis reduction method).
References
| [a1] | N. Alon, J. Spencer, "The probabilistic method" , Wiley (2000) (Edition: Second) |
| [a2] | J. Beck, "An algorithmic approach to the Lovász local lemma, I" , Random Structures and Algorithms , 2 (1991) pp. 343–365 |
| [a3] | P. Erdős, L. Lovász, "Problems and results on 3-chromatic hypergraphs and some related questions" A. Hajnal (ed.) et al. (ed.) , Infinite and Finite Sets , North-Holland (1975) pp. 609–628 |
Lovász local lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lov%C3%A1sz_local_lemma&oldid=16916