Legendre theorem
1) The indeterminate (Diophantine) equation
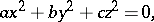 |
whose coefficients  ,
, 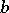 and
and  are pairwise coprime integers, square-free and not all of the same sign, has a non-zero rational solution if and only if all following three congruences (cf. Congruence) are solvable:
are pairwise coprime integers, square-free and not all of the same sign, has a non-zero rational solution if and only if all following three congruences (cf. Congruence) are solvable:
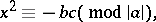 |
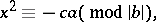 |
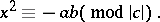 |
The question of representing the zeros of an arbitrary ternary quadratic form with rational coefficients reduces to Legendre's theorem.
It was proved by A.M. Legendre in 1785.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) pp. Chapt. 1. Par. 7 (Translated from Russian) (German translation: Birkhäuser, 1966) |
Comments
Legendre's theorem is an essential part of the Hasse–Minkowski theorem on rational quadratic forms (cf. Quadratic form).
2) The sum of the angles of a triangle cannot exceed two right angles.
3) If the sum of the angles of one triangle is equal to two right angles, then the sum of the angles of any other triangle is equal to two right angles.
Theorems 2) and 3) were proved by A.M. Legendre in 1800 and 1833 in attempts to justify Euclid's parallelism postulate (cf. Fifth postulate). Similar assertions were established by G. Saccheri (see Saccheri quadrangle).
References
| [1] | V.F. Kagan, "Foundations of geometry" , 1 , Moscow-Leningrad (1949) (In Russian) |
| [2] | A.V. Pogorelov, "Lectures on the foundations of geometry" , Noordhoff (1966) (Translated from Russian) |
A.B. Ivanov
Comments
References
| [a1] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
| [a2] | A.P. Norden, "Elementare Einführung in die Lobatschewskische Geometrie" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
Legendre theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Legendre_theorem&oldid=14807