L-variety
A class 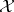 of
of 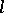 -groups (cf.
-groups (cf. 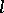 -group) that is distinguished within the class
-group) that is distinguished within the class 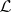 of all
of all 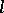 -groups by some system
-groups by some system 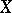 of
of 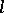 -group identities: an
-group identities: an 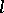 -group
-group 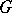 belongs to
belongs to 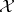 if and only if for all
if and only if for all 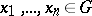 ,
,
 |
where 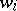 are terms in the variables
are terms in the variables  in the signature of
in the signature of 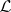 ,
, 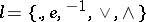 . (Cf. also Variety of groups.)
. (Cf. also Variety of groups.)
The class 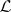 is defined by the following axiom system:
is defined by the following axiom system:
1) if 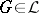 , then
, then 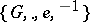 is a group;
is a group;
2) if 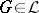 , then
, then 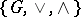 is a lattice;
is a lattice;
3) for all  ,
, 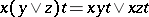 ;
;
4) for all  ,
, 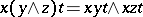 .
.
Any  -variety is closed under taking
-variety is closed under taking 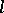 -subgroups,
-subgroups,  -homomorphisms, direct and Cartesian products, and is locally closed. If
-homomorphisms, direct and Cartesian products, and is locally closed. If  is an
is an 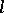 -group and
-group and 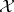 is an
is an 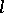 -variety, then there exists in
-variety, then there exists in 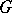 an
an 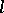 -ideal
-ideal 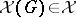 such that
such that 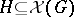 for every convex
for every convex 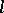 -subgroup
-subgroup 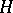 of
of 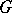 ,
, 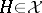 . For every
. For every 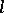 -variety
-variety 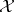 and set
and set 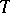 there exists an
there exists an 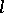 -group
-group 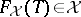 that is a free object in
that is a free object in 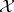 with set of generators
with set of generators 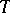 , i.e.,
, i.e., 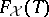 has the property: a mapping
has the property: a mapping 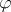 from
from 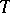 into the
into the 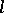 -group
-group 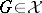 , can be extended to an
, can be extended to an  -homomorphism from
-homomorphism from 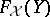 into
into 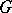 . There exists a description of the free
. There exists a description of the free 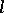 -groups
-groups 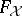 in terms of
in terms of 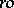 -groups and groups
-groups and groups 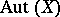 of order automorphisms of a suitable totally ordered set
of order automorphisms of a suitable totally ordered set 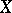 (cf.
(cf. 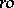 -group). The free
-group). The free 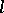 -group
-group 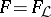 on
on 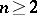 free generators has a faithful transitive representation in
free generators has a faithful transitive representation in 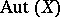 for some
for some 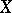 . It is a group with unique roots and orderable.
. It is a group with unique roots and orderable.
The most important 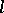 -varieties are as follows: a) the class of Abelian
-varieties are as follows: a) the class of Abelian 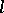 -groups
-groups 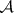 ; b) the class of the normal-valued
; b) the class of the normal-valued 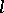 -groups
-groups 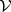 ; and c) the class of representable
; and c) the class of representable 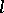 -groups
-groups 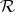 .
.
The  -variety
-variety 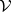 is distinguished in
is distinguished in 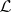 by the identity
by the identity
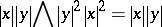 |
(here, 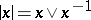 ). An
). An  -group
-group  belongs to
belongs to 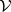 if and only if for any jump
if and only if for any jump 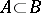 in the lattice
in the lattice 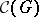 of convex subgroups of
of convex subgroups of 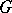 one has:
one has: 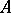 is an
is an 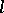 -ideal of
-ideal of  and the quotient group
and the quotient group 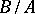 is Abelian. If
is Abelian. If 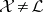 for an
for an 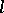 -variety
-variety 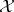 , then
, then 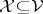 .
.
The 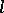 -variety
-variety 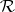 is distinguished in
is distinguished in  by the identity
by the identity 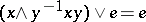 . An
. An 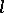 -group
-group 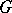 belongs to
belongs to 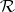 if and only if
if and only if  is an
is an 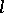 -subgroup of a Cartesian product of
-subgroup of a Cartesian product of  -groups. If
-groups. If 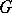 is a locally nilpotent
is a locally nilpotent 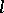 -group, then
-group, then 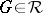 .
.
The set of all 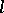 -varieties is a complete distributive lattice. The power of this lattice is the continuum. For any
-varieties is a complete distributive lattice. The power of this lattice is the continuum. For any 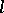 -variety
-variety  there exists an
there exists an 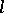 -variety
-variety 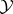 such that
such that 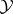 covers
covers 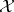 in the lattice of
in the lattice of 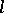 -varieties. The set of all covers of
-varieties. The set of all covers of 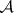 has been described.
has been described.
References
| [a1] | "Lattice-ordered groups: advances and techniques" A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Kluwer Acad. Publ. (1989) |
| [a2] | V.M. Kopytov, N.Ya. Medvedev, "The theory of lattice-ordered groups" , Kluwer Acad. Publ. (1994) (In Russian) |
L-variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-variety&oldid=18744