Difference between revisions of "Kontsevich integral"
(Importing text file) |
(details) |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 82 formulas, 75 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | An integral giving the universal Vassiliev knot invariant. Any Vassiliev knot invariant [[#References|[a6]]] can be derived from it. The integral is defined for a knot $K$ (cf. also [[Knot theory|Knot theory]]) embedded in the three-dimensional space $ \mathbf{R} ^ { 3 } = \mathbf{C} _ { z } \times \mathbf{R} _ { t }$ in such a way that the coordinate $t$ is a [[Morse function|Morse function]] on $K$ (all critical points are non-degenerate and all critical levels are different). Its values belong to the graded completion $\overline{\mathcal{A}}$ of the algebra of chord diagrams $\mathcal{A}$ defined below. | ||
| + | |||
| + | The Kontsevich integral $Z ( K )$ is an iterated integral given by the formula: | ||
| + | |||
| + | \begin{equation*} \sum _ { m = 0 } ^ { \infty } \frac { 1 } { ( 2 \pi i ) ^ { m } } \int _ { T } \sum _ { P = \{ ( z _ { j } , z _ { j } ^ { \prime } ) \} } ( - 1 ) ^ { \downarrow } D _ { P } \bigwedge _ { j = 1 } ^ { m } \frac { d z _ { j } - d z _ { j } ^ { \prime } } { z _ { j } - z _ { j } ^ { \prime } }. \end{equation*} | ||
The ingredients of this formula are as follows: | The ingredients of this formula are as follows: | ||
| − | 1) The real numbers | + | 1) The real numbers $t_\text{min}$ and $t_\text{max}$ are the minimum and the maximum of the function $t$ on $K$. |
| − | 2) The integration domain | + | 2) The integration domain $T$ is the $m$-dimensional simplex $t _ { \operatorname { min } } < t _ { 1 } < \ldots < t _ { m } < t _ { \operatorname { max } }$ divided by the critical values into a certain number of connected components; $T = \{ ( t _ { 1 } , \dots , t _ { m } ) : t _ { \operatorname { min } } < t _ { 1 } < \ldots < t _ { m } < t _ { \operatorname { max } } ,\; t_{j} \text{non critical} \}$. |
| − | 3) The number of summands in the integrand is constant in each connected component of the integration domain, but can be different for different components. Each plane | + | 3) The number of summands in the integrand is constant in each connected component of the integration domain, but can be different for different components. Each plane $\{ t = t _ { j } \} \subset \mathbf{R} ^ { 3 }$ intersects the knot $K$ in some number, say $n_j$, of points. The numbers $n_j$ are constants if $( t _ { 1 } , \dots , t _ { m } )$ belongs to a fixed connected component of the integration domain, but in general they can be different for different components. Choose one of $\left( \begin{array} { c } { n_j } \\ { 2 } \end{array} \right)$ unordered pairs of distinct points $( z _ { j } , t _ { j } )$ and $( z _ { j } ^ { \prime } , t _ { j } )$ on $\{ t = t_j \} \cup K$ for each $j$. Denote by $P = \{ ( z _ { j } , z _ { j } ^ { \prime } ) \}$ a set of such pairs for all $j = 1 , \ldots , m$. The integrand is the sum over all choices $P$. |
| − | 4) For a pairing | + | 4) For a pairing $P$ the symbol $\downarrow$ denotes the number of points $( z _ { j } , t _ { j } )$ or $( z _ { j } ^ { \prime } , t _ { j } )$ in $P$ where the coordinate $t$ decreases along the orientation of $K$. |
| − | 5) Fix a pairing | + | 5) Fix a pairing $P$. Consider the knot $K$ as an oriented circle and connect the points $( z _ { j } , t _ { j } )$ and $( z _ { j } ^ { \prime } , t _ { j } )$ by a chord. One obtains a chord diagram with $m$ chords. The corresponding element of the algebra $\mathcal{A}$ is denoted by $D _ { P }$. The algebra of chord diagrams $\mathcal{A}$ is the [[Graded algebra|graded algebra]] $\mathcal{A} = \mathcal{A} _ { 0 } \oplus \mathcal{A} _ { 1 } \oplus \ldots$. The linear space $\mathcal{A} _ { m }$ is generated over $\mathbf{C}$ by all chord diagrams with $m$ chords considered modulo the relations of the following two types: |
One-term relations: | One-term relations: | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k120100a.gif" style="border:1px solid;"/> |
Figure: k120100a | Figure: k120100a | ||
| Line 27: | Line 35: | ||
Four-term relations: | Four-term relations: | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k120100b.gif" style="border:1px solid;"/> |
Figure: k120100b | Figure: k120100b | ||
| − | for an arbitrary fixed position of | + | for an arbitrary fixed position of $( n - 2 )$ chords (which are not drawn here) and the two additional chords positioned as shown in the picture. |
| − | The multiplication in | + | The multiplication in $\mathcal{A}$ is defined by the connected sum of chord diagrams, which is well-defined thanks to the four-term relations. In fact $\mathcal{A}$ is even a [[Hopf algebra|Hopf algebra]] but the co-multiplication is not needed here. |
| − | 6) Over each connected component, | + | 6) Over each connected component, $z_j$ and $z _ { j } ^ { \prime }$ are smooth functions in $t_j$. With some abuse of notation, |
| − | + | \begin{equation*} \bigwedge _ { j = 1 } ^ { m } \frac { d z _ { j } - d z _ { j } ^ { \prime } } { z _ { j } - z _ { j } ^ { \prime } } \end{equation*} | |
| − | is to be interpreted as the pullback of this form to the integration domain of variables | + | is to be interpreted as the pullback of this form to the integration domain of variables $t _ { 1 } , \ldots , t _ { m }$. The integration domain is considered with the positive orientation of the space $\mathbf{R} ^ { m }$ defined by the natural order of the coordinates $t _ { 1 } , \ldots , t _ { m }$. |
| − | 7) By convention, the term in the Kontsevich integral corresponding to | + | 7) By convention, the term in the Kontsevich integral corresponding to $m = 0$ is the (only) chord diagram of order $0$ (without chords) with coefficient one. It represents the unit of the algebra $\mathcal{A}$. |
| − | The Kontsevich integral is convergent thanks to the one-term relations. It is invariant under deformations of a knot | + | The Kontsevich integral is convergent thanks to the one-term relations. It is invariant under deformations of a knot $K$ in the class of Morse knots. Unfortunately, the Kontsevich integral is not invariant under deformations that change the number of critical points of the function $t$. However, the following formula shows how the integral changes under such deformations: |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k120100c.gif" style="border:1px solid;"/> |
Figure: k120100c | Figure: k120100c | ||
| − | Here, the first and the third pictures depict an arbitrary knot, differing only in the fragment shown, while the second picture represents the unknot embedded in | + | Here, the first and the third pictures depict an arbitrary knot, differing only in the fragment shown, while the second picture represents the unknot embedded in $\mathbf{R} ^ { 3 }$ in the specified way and the product is the product in the completed algebra $\overline{\mathcal{A}}$ of chord diagrams. The last equality allows one to define the universal Vassiliev invariant by the formula |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k120100d.gif" style="border:1px solid;"/> |
Figure: k120100d | Figure: k120100d | ||
| − | Here, | + | Here, $c$ denotes the number of critical points of $K$ and the quotient means division in the algebra $\overline{\mathcal{A}}$: |
| − | + | \begin{equation*} ( 1 + a ) ^ { - 1 } = 1 - a + a ^ { 2 } - a ^ { 3 } +\dots . \end{equation*} | |
| − | The universal Vassiliev invariant | + | The universal Vassiliev invariant $\tilde{Z} ( K )$ is invariant under an arbitrary deformation of $K$. |
| − | Consider a function | + | Consider a function $w$ on the set of chord diagrams with $m$ chords satisfying one- and four-term relations. Applying this function to the universal Vassiliev invariant $w ( \widetilde{Z} ( K ) )$, one obtains a numerical knot invariant. This invariant will be a Vassiliev invariant of order $m$ and any Vassiliev invariant can be obtained in this way. The Kontsevich integral is extremely complicated. For a long time even the Kontsevich integral of the unknot |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/k120100e.gif" style="border:1px solid;"/> |
Figure: k120100e | Figure: k120100e | ||
| Line 69: | Line 77: | ||
was unknown. The conjecture about it appeared only recently [[#References|[a7]]]. D. Bar-Natan, T. Le and D. Thurston proved the conjecture but the preprint is still in preparation (1999). | was unknown. The conjecture about it appeared only recently [[#References|[a7]]]. D. Bar-Natan, T. Le and D. Thurston proved the conjecture but the preprint is still in preparation (1999). | ||
| − | The Kontsevich integral behaves in a nice way with respect to the natural operations on knots, such as mirror reflection, changing the orientation of the knot, and mutation of knots. It is multiplicative under the connected sum of knots (because it is a group-like element in the Hopf algebra | + | The Kontsevich integral behaves in a nice way with respect to the natural operations on knots, such as mirror reflection, changing the orientation of the knot, and mutation of knots. It is multiplicative under the connected sum of knots (because it is a group-like element in the Hopf algebra $\overline{\mathcal{A}}$). The claim that the coefficients of $Z ( K )$ are rational, [[#References|[a5]]], was proved in [[#References|[a4]]]. |
The Kontsevich integral was invented by M. Kontsevich [[#References|[a5]]]. See [[#References|[a1]]], [[#References|[a2]]], [[#References|[a3]]] for detailed expositions of the relevant theory. | The Kontsevich integral was invented by M. Kontsevich [[#References|[a5]]]. See [[#References|[a1]]], [[#References|[a2]]], [[#References|[a3]]] for detailed expositions of the relevant theory. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> V.I. Arnol'd, "Vassiliev's theory of discriminants and knots" , ''First European Congress of Mathematicians (Paris)'' , Birkhäuser (1992) pp. 3–29 {{ZBL|0869.57006}}</td></tr> | ||
| + | <tr><td valign="top">[a2]</td> <td valign="top"> D. Bar-Natan, "On the Vassiliev knot invariants" ''Topology'' , '''34''' (1995) pp. 423–472 {{MR|}} {{ZBL|0898.57001}} </td></tr> | ||
| + | <tr><td valign="top">[a3]</td> <td valign="top"> S.V. Chmutov, S.V. Duzhin, "The Kontsevich integral" ''Acta Applic. Math.'' (to appear) (available via anonymous ftp: pier.botik.ru, file: pub/local/zmr/ki.ps.gz) {{MR|1837618}} {{ZBL|0980.57006}} </td></tr> | ||
| + | <tr><td valign="top">[a4]</td> <td valign="top"> T.Q.T. Le, J. Murakami, "The universal Vassiliev-Kontsevich invariant for framed oriented links" ''Compositio Math.'' , '''102''' (1996) pp. 42–64 {{MR|1394520}} {{ZBL|0851.57007}} </td></tr> | ||
| + | <tr><td valign="top">[a5]</td> <td valign="top"> M. Kontsevich, "Vassiliev's knot invariants" ''Adv. Soviet Math.'' , '''16''' (1993) pp. 137–150 {{MR|1237836}} {{ZBL|}} </td></tr> | ||
| + | <tr><td valign="top">[a6]</td> <td valign="top"> V.A. Vassiliev, "Theory of singularities and its applications" V.I. Arnol'd) (ed.) , ''Advances in Soviet Math.'' , '''1''' , Amer. Math. Soc. (1990) pp. 23 –69</td></tr> | ||
| + | <tr><td valign="top">[a7]</td> <td valign="top"> D. Bar-Natan, S. Garoufalidis, L. Rozansky, D. Thurston, "Wheels, wheeling, and the Kontsevich integral of the unknot" ''preprint'' , '''March''' (1997) pp. q–alg/9703025 {{MR|}} {{ZBL|0964.57010}} </td></tr></table> | ||
| + | |||
| + | {{OldImage}} | ||
Latest revision as of 19:05, 23 January 2024
An integral giving the universal Vassiliev knot invariant. Any Vassiliev knot invariant [a6] can be derived from it. The integral is defined for a knot $K$ (cf. also Knot theory) embedded in the three-dimensional space $ \mathbf{R} ^ { 3 } = \mathbf{C} _ { z } \times \mathbf{R} _ { t }$ in such a way that the coordinate $t$ is a Morse function on $K$ (all critical points are non-degenerate and all critical levels are different). Its values belong to the graded completion $\overline{\mathcal{A}}$ of the algebra of chord diagrams $\mathcal{A}$ defined below.
The Kontsevich integral $Z ( K )$ is an iterated integral given by the formula:
\begin{equation*} \sum _ { m = 0 } ^ { \infty } \frac { 1 } { ( 2 \pi i ) ^ { m } } \int _ { T } \sum _ { P = \{ ( z _ { j } , z _ { j } ^ { \prime } ) \} } ( - 1 ) ^ { \downarrow } D _ { P } \bigwedge _ { j = 1 } ^ { m } \frac { d z _ { j } - d z _ { j } ^ { \prime } } { z _ { j } - z _ { j } ^ { \prime } }. \end{equation*}
The ingredients of this formula are as follows:
1) The real numbers $t_\text{min}$ and $t_\text{max}$ are the minimum and the maximum of the function $t$ on $K$.
2) The integration domain $T$ is the $m$-dimensional simplex $t _ { \operatorname { min } } < t _ { 1 } < \ldots < t _ { m } < t _ { \operatorname { max } }$ divided by the critical values into a certain number of connected components; $T = \{ ( t _ { 1 } , \dots , t _ { m } ) : t _ { \operatorname { min } } < t _ { 1 } < \ldots < t _ { m } < t _ { \operatorname { max } } ,\; t_{j} \text{non critical} \}$.
3) The number of summands in the integrand is constant in each connected component of the integration domain, but can be different for different components. Each plane $\{ t = t _ { j } \} \subset \mathbf{R} ^ { 3 }$ intersects the knot $K$ in some number, say $n_j$, of points. The numbers $n_j$ are constants if $( t _ { 1 } , \dots , t _ { m } )$ belongs to a fixed connected component of the integration domain, but in general they can be different for different components. Choose one of $\left( \begin{array} { c } { n_j } \\ { 2 } \end{array} \right)$ unordered pairs of distinct points $( z _ { j } , t _ { j } )$ and $( z _ { j } ^ { \prime } , t _ { j } )$ on $\{ t = t_j \} \cup K$ for each $j$. Denote by $P = \{ ( z _ { j } , z _ { j } ^ { \prime } ) \}$ a set of such pairs for all $j = 1 , \ldots , m$. The integrand is the sum over all choices $P$.
4) For a pairing $P$ the symbol $\downarrow$ denotes the number of points $( z _ { j } , t _ { j } )$ or $( z _ { j } ^ { \prime } , t _ { j } )$ in $P$ where the coordinate $t$ decreases along the orientation of $K$.
5) Fix a pairing $P$. Consider the knot $K$ as an oriented circle and connect the points $( z _ { j } , t _ { j } )$ and $( z _ { j } ^ { \prime } , t _ { j } )$ by a chord. One obtains a chord diagram with $m$ chords. The corresponding element of the algebra $\mathcal{A}$ is denoted by $D _ { P }$. The algebra of chord diagrams $\mathcal{A}$ is the graded algebra $\mathcal{A} = \mathcal{A} _ { 0 } \oplus \mathcal{A} _ { 1 } \oplus \ldots$. The linear space $\mathcal{A} _ { m }$ is generated over $\mathbf{C}$ by all chord diagrams with $m$ chords considered modulo the relations of the following two types:
One-term relations:
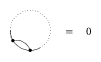
Figure: k120100a
(here and below, the dotted arcs suggest that there might be further chords attached to their points, while on the solid portions of the circle all the endpoints are explicitly shown); and
Four-term relations:
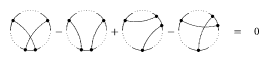
Figure: k120100b
for an arbitrary fixed position of $( n - 2 )$ chords (which are not drawn here) and the two additional chords positioned as shown in the picture.
The multiplication in $\mathcal{A}$ is defined by the connected sum of chord diagrams, which is well-defined thanks to the four-term relations. In fact $\mathcal{A}$ is even a Hopf algebra but the co-multiplication is not needed here.
6) Over each connected component, $z_j$ and $z _ { j } ^ { \prime }$ are smooth functions in $t_j$. With some abuse of notation,
\begin{equation*} \bigwedge _ { j = 1 } ^ { m } \frac { d z _ { j } - d z _ { j } ^ { \prime } } { z _ { j } - z _ { j } ^ { \prime } } \end{equation*}
is to be interpreted as the pullback of this form to the integration domain of variables $t _ { 1 } , \ldots , t _ { m }$. The integration domain is considered with the positive orientation of the space $\mathbf{R} ^ { m }$ defined by the natural order of the coordinates $t _ { 1 } , \ldots , t _ { m }$.
7) By convention, the term in the Kontsevich integral corresponding to $m = 0$ is the (only) chord diagram of order $0$ (without chords) with coefficient one. It represents the unit of the algebra $\mathcal{A}$.
The Kontsevich integral is convergent thanks to the one-term relations. It is invariant under deformations of a knot $K$ in the class of Morse knots. Unfortunately, the Kontsevich integral is not invariant under deformations that change the number of critical points of the function $t$. However, the following formula shows how the integral changes under such deformations:
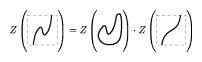
Figure: k120100c
Here, the first and the third pictures depict an arbitrary knot, differing only in the fragment shown, while the second picture represents the unknot embedded in $\mathbf{R} ^ { 3 }$ in the specified way and the product is the product in the completed algebra $\overline{\mathcal{A}}$ of chord diagrams. The last equality allows one to define the universal Vassiliev invariant by the formula
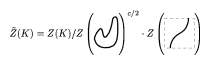
Figure: k120100d
Here, $c$ denotes the number of critical points of $K$ and the quotient means division in the algebra $\overline{\mathcal{A}}$:
\begin{equation*} ( 1 + a ) ^ { - 1 } = 1 - a + a ^ { 2 } - a ^ { 3 } +\dots . \end{equation*}
The universal Vassiliev invariant $\tilde{Z} ( K )$ is invariant under an arbitrary deformation of $K$.
Consider a function $w$ on the set of chord diagrams with $m$ chords satisfying one- and four-term relations. Applying this function to the universal Vassiliev invariant $w ( \widetilde{Z} ( K ) )$, one obtains a numerical knot invariant. This invariant will be a Vassiliev invariant of order $m$ and any Vassiliev invariant can be obtained in this way. The Kontsevich integral is extremely complicated. For a long time even the Kontsevich integral of the unknot
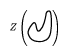
Figure: k120100e
was unknown. The conjecture about it appeared only recently [a7]. D. Bar-Natan, T. Le and D. Thurston proved the conjecture but the preprint is still in preparation (1999).
The Kontsevich integral behaves in a nice way with respect to the natural operations on knots, such as mirror reflection, changing the orientation of the knot, and mutation of knots. It is multiplicative under the connected sum of knots (because it is a group-like element in the Hopf algebra $\overline{\mathcal{A}}$). The claim that the coefficients of $Z ( K )$ are rational, [a5], was proved in [a4].
The Kontsevich integral was invented by M. Kontsevich [a5]. See [a1], [a2], [a3] for detailed expositions of the relevant theory.
References
| [a1] | V.I. Arnol'd, "Vassiliev's theory of discriminants and knots" , First European Congress of Mathematicians (Paris) , Birkhäuser (1992) pp. 3–29 Zbl 0869.57006 |
| [a2] | D. Bar-Natan, "On the Vassiliev knot invariants" Topology , 34 (1995) pp. 423–472 Zbl 0898.57001 |
| [a3] | S.V. Chmutov, S.V. Duzhin, "The Kontsevich integral" Acta Applic. Math. (to appear) (available via anonymous ftp: pier.botik.ru, file: pub/local/zmr/ki.ps.gz) MR1837618 Zbl 0980.57006 |
| [a4] | T.Q.T. Le, J. Murakami, "The universal Vassiliev-Kontsevich invariant for framed oriented links" Compositio Math. , 102 (1996) pp. 42–64 MR1394520 Zbl 0851.57007 |
| [a5] | M. Kontsevich, "Vassiliev's knot invariants" Adv. Soviet Math. , 16 (1993) pp. 137–150 MR1237836 |
| [a6] | V.A. Vassiliev, "Theory of singularities and its applications" V.I. Arnol'd) (ed.) , Advances in Soviet Math. , 1 , Amer. Math. Soc. (1990) pp. 23 –69 |
| [a7] | D. Bar-Natan, S. Garoufalidis, L. Rozansky, D. Thurston, "Wheels, wheeling, and the Kontsevich integral of the unknot" preprint , March (1997) pp. q–alg/9703025 Zbl 0964.57010 |
Kontsevich integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kontsevich_integral&oldid=16302