Hopf-Tsuji-Sullivan theorem
This theorem establishes the equivalence of several characterizations of "smallness" of a Riemannian manifold of constant negative curvature, or, more generally, of a discrete group 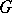 of isometries of the
of isometries of the 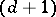 -dimensional hyperbolic space
-dimensional hyperbolic space 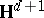 (cf. also Discrete group of transformations).
(cf. also Discrete group of transformations).
Denote by 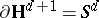 the sphere at infinity (the visibility sphere), of
the sphere at infinity (the visibility sphere), of 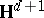 , and fix an origin
, and fix an origin 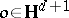 . A point
. A point 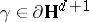 is called a radial limit point of the group
is called a radial limit point of the group 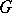 if there exists a number
if there exists a number 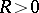 such that the
such that the 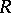 -neighbourhood of the geodesic ray
-neighbourhood of the geodesic ray 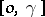 contains infinitely many points from the orbit
contains infinitely many points from the orbit 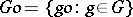 . The set
. The set 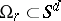 of all radial limit points is called the radial limit set of
of all radial limit points is called the radial limit set of 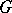 . Alternatively, let the shadow
. Alternatively, let the shadow 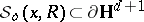 of the ball
of the ball 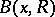 of radius
of radius 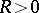 centred at a point
centred at a point 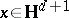 be the set of end-points of all geodesic rays which are issued from
be the set of end-points of all geodesic rays which are issued from  and intersect
and intersect 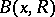 . Then
. Then 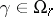 if and only if there is an
if and only if there is an 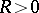 such that
such that 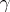 belongs to an infinite number of shadows
belongs to an infinite number of shadows 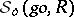 ,
, 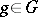 .
.
The following conditions are equivalent:
1) The Poincaré series 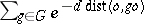 diverges, where
diverges, where 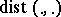 is the Riemannian distance on
is the Riemannian distance on 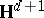 .
.
2) The quotient 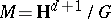 has no Green function, i.e.,
has no Green function, i.e., 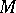 has no non-constant negative subharmonic functions (cf. also Subharmonic function), or, equivalently, the Brownian motion on
has no non-constant negative subharmonic functions (cf. also Subharmonic function), or, equivalently, the Brownian motion on 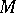 is recurrent.
is recurrent.
3) The complement of the radial limit set 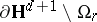 has Lebesgue measure zero.
has Lebesgue measure zero.
4) The geodesic flow on 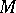 is ergodic with respect to the Liouville-invariant measure (the one determined by the Riemannian volume).
is ergodic with respect to the Liouville-invariant measure (the one determined by the Riemannian volume).
5) The action of 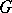 on the product
on the product 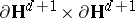 is ergodic with respect to the Lebesgue measure.
is ergodic with respect to the Lebesgue measure.
Usually the term "Hopf–Tsuji–Sullivan theorem" is applied to the equivalence of 1), 3) and 4). For 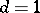 the implication 3)
the implication 3)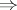 4) was first proved by E. Hopf [a1], [a2], and the implications 4)
4) was first proved by E. Hopf [a1], [a2], and the implications 4)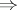 1)
1)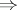 3) by M. Tsuji, see [a3]. Tsuji's proof is essentially
3) by M. Tsuji, see [a3]. Tsuji's proof is essentially  -dimensional, as it uses complex function theory, whereas Hopf's argument easily carries over to the higher-dimensional case. D. Sullivan [a4] used an entirely different way for proving the chain of implications 4)
-dimensional, as it uses complex function theory, whereas Hopf's argument easily carries over to the higher-dimensional case. D. Sullivan [a4] used an entirely different way for proving the chain of implications 4)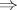 3)
3)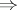 1)
1)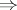 4) for an arbitrary dimension
4) for an arbitrary dimension 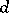 .
.
The equivalence of 1) and 2) follows from the asymptotic equivalence of the Green function on 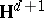 to
to 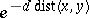 , whereas the equivalence of 3), 4) and 5) is a much more general fact, see Hopf alternative. Sullivan's idea was to deduce the implication 2)
, whereas the equivalence of 3), 4) and 5) is a much more general fact, see Hopf alternative. Sullivan's idea was to deduce the implication 2)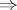 5) from general properties of recurrent Markov operators. On the other hand, the implication 3)
5) from general properties of recurrent Markov operators. On the other hand, the implication 3)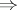 1) is an easy corollary of the estimate
1) is an easy corollary of the estimate 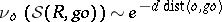 , where
, where 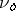 is the image of the Lebesgue measure on the unit tangent sphere at the point
is the image of the Lebesgue measure on the unit tangent sphere at the point  under the exponential mapping (a particular case of the Sullivan shadow lemma).
under the exponential mapping (a particular case of the Sullivan shadow lemma).
Ergodicity of the action of 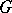 on
on 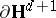 (i.e., absence of bounded harmonic functions on
(i.e., absence of bounded harmonic functions on 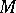 ) is weaker than 5). For Riemannian surfaces the implication "no Green function"
) is weaker than 5). For Riemannian surfaces the implication "no Green function" 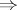 "no non-constant bounded harmonic functions" is known as the Myrberg theorem, see [a5]. In probabilistic terms, this implication can be reformulated as "ergodicity of the time shift in the bilateral path space"
"no non-constant bounded harmonic functions" is known as the Myrberg theorem, see [a5]. In probabilistic terms, this implication can be reformulated as "ergodicity of the time shift in the bilateral path space" 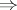 "ergodicity of the time shift in the unilateral path space" , or just that recurrence of the Brownian motion
"ergodicity of the time shift in the unilateral path space" , or just that recurrence of the Brownian motion 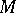 implies absence of non-constant bounded harmonic functions [a6]. The latter reformulation allows one to construct examples of discrete groups of isometries of
implies absence of non-constant bounded harmonic functions [a6]. The latter reformulation allows one to construct examples of discrete groups of isometries of 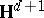 whose action on
whose action on 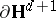 is ergodic and on
is ergodic and on 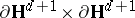 is not, in a much simpler way than original Riemann surface examples, [a7].
is not, in a much simpler way than original Riemann surface examples, [a7].
An analogue of the Hopf–Tsuji–Sullivan theorem for the invariant measure of the geodesic flow corresponding to the Patterson–Sullivan measure on 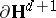 was proved in [a8], see also [a9]. In this setup, condition 1) is replaced by divergence of the Poincaré series at the critical exponent of the group
was proved in [a8], see also [a9]. In this setup, condition 1) is replaced by divergence of the Poincaré series at the critical exponent of the group 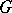 .
.
In the non-constant curvature case, generalizations of the Hopf–Tsuji–Sullivan theorem were obtained in [a6] for the harmonic invariant measure of the geodesic flow and in [a10] for the Patterson–Sullivan measure.
References
| [a1] | E. Hopf, "Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krummung" Ber. Verh. Sachs. Akad. Wiss. Leipzig , 91 (1939) pp. 261–304 |
| [a2] | E. Hopf, "Ergodic theory and the geodesic flow on surfaces of constant negative curvature" Bull. Amer. Math. Soc. , 77 (1971) pp. 863–877 |
| [a3] | M. Tsuji, "Potential theory in modern function theory" , Maruzen (1959) |
| [a4] | D. Sullivan, "On the ergodic theory at infinity of an arbitrary discrete group of hyperbolic motions" Ann. Math. Studies , 97 (1980) pp. 465–496 |
| [a5] | L.V. Ahlfors, L. Sario, "Riemann surfaces" , Princeton Univ. Press (1960) |
| [a6] | V.A. Kaimanovich, "Ergodicity of harmonic invariant measures for the geodesic flow on hyperbolic spaces" J. Reine Angew. Math. , 455 (1994) pp. 57–103 |
| [a7] | T. Lyons, D. Sullivan, "Function theory, random paths and covering spaces" J. Diff. Geom. , 19 (1984) pp. 299–323 |
| [a8] | D. Sullivan, "The density at infinity of a discrete group of hyperbolic motions" IHES Publ. Math. , 50 (1979) pp. 171–202 |
| [a9] | P.J. Nicholls, "Ergodic theory of discrete groups" , Cambridge Univ. Press (1989) |
| [a10] | C.B. Yue, "The ergodic theory of discrete isometry groups on manifolds of variable negative curvature" Trans. Amer. Math. Soc. , 348 (1996) pp. 4965–5005 |
Hopf-Tsuji-Sullivan theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf-Tsuji-Sullivan_theorem&oldid=18178