Cubature formula
A formula for the approximate calculation of multiple integrals of the form
 |
The integration is performed over a set  in the Euclidean space
in the Euclidean space 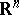 ,
, 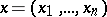 . A cubature formula is an approximate equality
. A cubature formula is an approximate equality
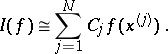 | (1) |
The integrand is written as the product of two functions: the first, 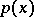 , is assumed to be fixed for each specific cubature formula and is known as a weight function; the second,
, is assumed to be fixed for each specific cubature formula and is known as a weight function; the second, 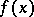 , is assumed to belong to some fairly broad class of functions, e.g. continuous functions such that the integral
, is assumed to belong to some fairly broad class of functions, e.g. continuous functions such that the integral 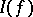 exists. The sum on the right-hand side of (1) is called a cubature sum; the points
exists. The sum on the right-hand side of (1) is called a cubature sum; the points  are known as the interpolation points (knots, nodes) of the formula, and the numbers
are known as the interpolation points (knots, nodes) of the formula, and the numbers 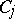 as its coefficients. Usually
as its coefficients. Usually 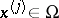 , though this condition is not necessary. In order to compute the integral
, though this condition is not necessary. In order to compute the integral 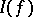 via formula (1), one need only calculate the cubature sum. If
via formula (1), one need only calculate the cubature sum. If  formula (1) and the sum on its right-hand side are known as a quadrature formula and sum (see Quadrature formula).
formula (1) and the sum on its right-hand side are known as a quadrature formula and sum (see Quadrature formula).
Let 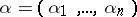 be a multi-index, where the
be a multi-index, where the 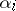 are non-negative integers; let
are non-negative integers; let 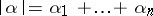 ; and let
; and let 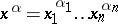 be a monomial of degree
be a monomial of degree 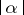 in
in  variables; let
variables; let
 |
be the number of monomials of degree at most 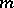 in
in  variables; let
variables; let  ,
, 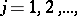 be an ordering of all monomials such that monomials of lower degree have lower subscript while the monomials of equal degree have been ordered arbitrarily, e.g. in lexicographical order. In this enumeration
be an ordering of all monomials such that monomials of lower degree have lower subscript while the monomials of equal degree have been ordered arbitrarily, e.g. in lexicographical order. In this enumeration 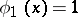 , and the
, and the 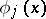 ,
, 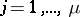 , include all monomials of degree at most
, include all monomials of degree at most 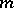 . Let
. Let 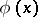 be a polynomial of degree
be a polynomial of degree 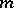 . The set of points in the complex space
. The set of points in the complex space 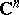 satisfying the equation
satisfying the equation 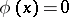 is known as an algebraic hypersurface of degree
is known as an algebraic hypersurface of degree 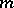 .
.
One way to construct cubature formulas is based on algebraic interpolation. The points 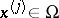 ,
, 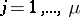 , are so chosen that they do not lie on any algebraic hypersurface of degree
, are so chosen that they do not lie on any algebraic hypersurface of degree 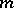 or, equivalently, they are chosen such that the Vandermonde matrix
or, equivalently, they are chosen such that the Vandermonde matrix
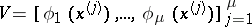 |
is non-singular. The Lagrange interpolation polynomial for a function 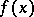 with knots
with knots 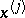 has the form
has the form
 |
where  is the polynomial of the influence of the
is the polynomial of the influence of the 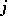 -th knot:
-th knot: 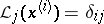 (
(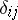 is the Kronecker symbol). Multiplying the approximate equality
is the Kronecker symbol). Multiplying the approximate equality 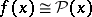 by
by 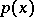 and integrating over
and integrating over  leads to a cubature formula of type (1) with
leads to a cubature formula of type (1) with 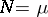 and
and
 | (2) |
The existence of the integrals (2) is equivalent to the existence of the moments of the weight function, 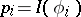 ,
,  . Here and below it is assumed that the required moments of
. Here and below it is assumed that the required moments of 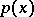 exist. A cubature formula (1) which has
exist. A cubature formula (1) which has  knots not contained in any algebraic hypersurface of degree
knots not contained in any algebraic hypersurface of degree 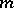 and with coefficients defined by (2), is called an interpolatory cubature formula. Formula (1) has the
and with coefficients defined by (2), is called an interpolatory cubature formula. Formula (1) has the 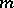 -property if it is an exact equality whenever
-property if it is an exact equality whenever 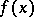 is a polynomial of degree at most
is a polynomial of degree at most  ; an interpolatory cubature formula has the
; an interpolatory cubature formula has the 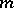 -property. A cubature formula (1) with
-property. A cubature formula (1) with 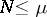 knots which has the
knots which has the 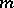 -property is an interpolatory formula if and only if the matrix
-property is an interpolatory formula if and only if the matrix
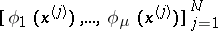 |
has rank 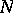 . This condition holds when
. This condition holds when 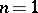 , so that a quadrature formula with
, so that a quadrature formula with  knots that has the
knots that has the 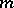 -property is an interpolatory formula. The actual construction of an interpolatory cubature formula reduces to a selection of the knots and a calculation of the coefficients. The coefficients
-property is an interpolatory formula. The actual construction of an interpolatory cubature formula reduces to a selection of the knots and a calculation of the coefficients. The coefficients 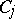 are determined by the linear algebraic system of equations
are determined by the linear algebraic system of equations
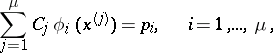 |
which is simply the mathematical expression of the statement that (1) (with  ) is exact for all monomials of degree at most
) is exact for all monomials of degree at most 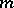 . The matrix of this system is precisely
. The matrix of this system is precisely 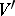 (
(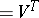 ).
).
Now suppose it is necessary to construct a cubature formula (1) with the  -property, but with less than
-property, but with less than 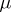 knots. Since this cannot be done by merely selecting the coefficients, not only the coefficients but also the knots are unknowns in (1), giving
knots. Since this cannot be done by merely selecting the coefficients, not only the coefficients but also the knots are unknowns in (1), giving 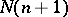 unknowns in total. Since the cubature formula must have the
unknowns in total. Since the cubature formula must have the 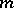 -property, one obtains
-property, one obtains 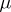 equations
equations
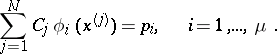 | (3) |
It is natural to require the number of unknowns to coincide with the number of equations: 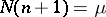 . This equation gives a tentative estimate of the number of knots. If
. This equation gives a tentative estimate of the number of knots. If 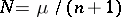 is not an integer, one puts
is not an integer, one puts 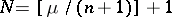 , where
, where 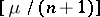 denotes the integer part of
denotes the integer part of 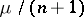 . A cubature formula with this number of knots need not always exist. If it does exist, its number of knots is
. A cubature formula with this number of knots need not always exist. If it does exist, its number of knots is  times the number of knots of an interpolatory cubature formula. In that case, however, the knots themselves and the coefficients are determined by the non-linear system of equations (3). In the method of undetermined parameters, one constructs a cubature formula by trying to give it a form that will simplify the system (3). This can be done when
times the number of knots of an interpolatory cubature formula. In that case, however, the knots themselves and the coefficients are determined by the non-linear system of equations (3). In the method of undetermined parameters, one constructs a cubature formula by trying to give it a form that will simplify the system (3). This can be done when  and
and 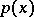 have symmetries. The positions of the knots are taken compatible with the symmetry of
have symmetries. The positions of the knots are taken compatible with the symmetry of  and
and 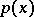 , and in that case symmetric knots are assigned the same coefficients. The simplification of the system (3) involves a certain risk: While the original system (3) may be solvable, the simplified system need not be.
, and in that case symmetric knots are assigned the same coefficients. The simplification of the system (3) involves a certain risk: While the original system (3) may be solvable, the simplified system need not be.
Example. Let 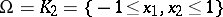 ,
, 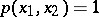 . One is asked to construct a cubature formula with the
. One is asked to construct a cubature formula with the 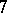 -property;
-property; 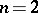 ,
, 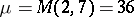 , and 12 knots. The knots are located as follows. The first group of knots consists of the intersection points of the circle of radius
, and 12 knots. The knots are located as follows. The first group of knots consists of the intersection points of the circle of radius  , centred at the origin, with the coordinate axes. The second group consists of the intersection points of the circle of radius
, centred at the origin, with the coordinate axes. The second group consists of the intersection points of the circle of radius 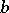 , also centred at the origin, with the straight lines
, also centred at the origin, with the straight lines 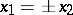 . The third group is constructed similarly, with radius denoted by
. The third group is constructed similarly, with radius denoted by  . The coefficients assigned to knots of the same group are identical and are denoted by
. The coefficients assigned to knots of the same group are identical and are denoted by 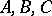 for knots of the first, second and third group, respectively. This choice of knots and coefficients implies that the cubature formula will be exact for monomials
for knots of the first, second and third group, respectively. This choice of knots and coefficients implies that the cubature formula will be exact for monomials  in which at least one of
in which at least one of 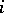 or
or 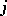 is odd. For the cubature formula to possess the
is odd. For the cubature formula to possess the 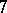 -property, it will suffice to ensure that it is exact for
-property, it will suffice to ensure that it is exact for 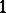 ,
, 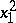 ,
,  ,
, 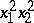 ,
, 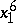 ,
,  . This yields a non-linear system of six equations in the six unknowns
. This yields a non-linear system of six equations in the six unknowns 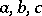 ,
, 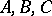 . Solving this system, one obtains a cubature formula with positive coefficients and with knots lying in
. Solving this system, one obtains a cubature formula with positive coefficients and with knots lying in 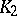 .
.
Let 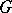 be a finite subgroup of the group of orthogonal transformations
be a finite subgroup of the group of orthogonal transformations  of the space
of the space 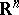 which leave the origin fixed. A set
which leave the origin fixed. A set  and a function
and a function 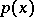 are said to be invariant under
are said to be invariant under  if
if 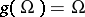 and
and 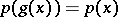 for
for 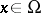 and any
and any 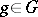 . The set of points of the form
. The set of points of the form 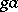 , where
, where  is a fixed point of
is a fixed point of  and
and 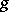 runs through all elements of
runs through all elements of  , is known as the orbit containing
, is known as the orbit containing  . A cubature formula (1) is said to be invariant under
. A cubature formula (1) is said to be invariant under  if
if  and
and 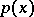 are invariant under
are invariant under 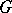 and if the set of knots is a union of orbits, with knots belonging to the same orbit being assigned identical coefficients. Examples of sets invariant under
and if the set of knots is a union of orbits, with knots belonging to the same orbit being assigned identical coefficients. Examples of sets invariant under 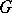 are the entire space
are the entire space  , and any ball or sphere centred at the origin; if
, and any ball or sphere centred at the origin; if  is the group of transformations of a regular polyhedron
is the group of transformations of a regular polyhedron 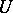 onto itself, then
onto itself, then 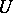 is also invariant. Thus, one can speak of invariant cubature formulas when
is also invariant. Thus, one can speak of invariant cubature formulas when  is
is  , a ball, a sphere, a cube or any regular polyhedron, and when
, a ball, a sphere, a cube or any regular polyhedron, and when 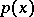 is any function invariant under
is any function invariant under  , e.g.
, e.g. 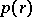 , where
, where 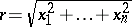 .
.
Theorem 1) A cubature formula which is invariant under  possesses the
possesses the 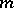 -property if and only if it is exact for all polynomials of degree at most
-property if and only if it is exact for all polynomials of degree at most 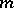 which are invariant under
which are invariant under  (see [5]). The method of undetermined coefficients may be defined as the method of constructing invariant cubature formulas possessing the
(see [5]). The method of undetermined coefficients may be defined as the method of constructing invariant cubature formulas possessing the 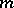 -property. In the above example, the role of the group
-property. In the above example, the role of the group 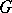 may be played by the symmetry group of the square. Theorem 1 is of essential importance in the construction of invariant cubature formulas.
may be played by the symmetry group of the square. Theorem 1 is of essential importance in the construction of invariant cubature formulas.
For simple domains of integration, such as a cube, a simplex, a ball, or a sphere, and for the weight 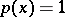 , one can construct cubature formulas by repeatedly using quadrature formulas. For example, when
, one can construct cubature formulas by repeatedly using quadrature formulas. For example, when 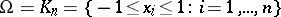 is the cube, one may use the Gauss quadrature formula with
is the cube, one may use the Gauss quadrature formula with 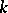 knots
knots 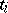 and coefficients
and coefficients 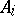 to obtain a cubature formula
to obtain a cubature formula
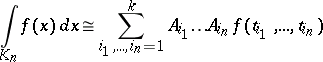 |
with 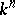 knots; this is exact for all monomials
knots; this is exact for all monomials 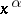 such that
such that 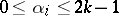 ,
, 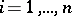 , and in particular for all polynomials of degree at most
, and in particular for all polynomials of degree at most 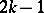 . The number of knots of such cubature formulas increases rapidly, a fact which limits their applicability.
. The number of knots of such cubature formulas increases rapidly, a fact which limits their applicability.
Throughout the sequel it will be assumed that the weight function is of fixed sign, say
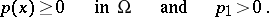 | (4) |
The fact that the coefficients of a cubature formula with such a weight function are positive, is a valuable property of the formula.
Theorem 2) If the domain of integration  is closed and
is closed and 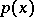 satisfies (4), there exists an interpolatory cubature formula (1) possessing the
satisfies (4), there exists an interpolatory cubature formula (1) possessing the 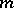 -property,
-property, 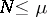 , with positive coefficients and with knots in
, with positive coefficients and with knots in  . The question of actually constructing such a formula is as yet open.
. The question of actually constructing such a formula is as yet open.
Theorem 3) If a cubature formula with a weight satisfying (4) has real knots and coefficients and possesses the 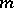 -property, then at least
-property, then at least 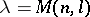 of its coefficients are positive, where
of its coefficients are positive, where 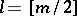 is the integer part of
is the integer part of 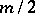 . Under the assumptions of Theorem 3, the number
. Under the assumptions of Theorem 3, the number 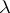 is a lower bound for the number of knots:
is a lower bound for the number of knots:
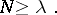 |
This inequality remains valid without the assumption that  and
and 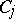 are real.
are real.
Regarding cubature formulas with the 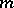 -property, one is particularly interested in those having a minimum number of knots. When
-property, one is particularly interested in those having a minimum number of knots. When 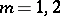 it is easy to find such formulas for any
it is easy to find such formulas for any  , arbitrary
, arbitrary  and
and 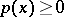 ; the minimum number of knots is precisely the lower bound
; the minimum number of knots is precisely the lower bound 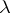 : It is equal to 1 in the first case, and to
: It is equal to 1 in the first case, and to 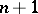 in the second. When
in the second. When 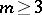 , the minimum number of knots depends on the domain and the weight. For example, if
, the minimum number of knots depends on the domain and the weight. For example, if 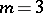 , the domain is centrally symmetric, and if
, the domain is centrally symmetric, and if 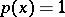 , the number of knots is
, the number of knots is 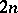 ; for a simplex and
; for a simplex and 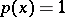 , it is
, it is 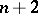 .
.
By virtue of (4),
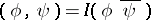 | (5) |
is a scalar product in the space of polynomials. Let 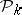 be the vector space of polynomials of degree
be the vector space of polynomials of degree 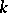 which are orthogonal in the sense of (5) to all polynomials of degree at most
which are orthogonal in the sense of (5) to all polynomials of degree at most 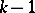 . This space has dimension
. This space has dimension  — the number of monomials of degree
— the number of monomials of degree 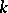 . Polynomials in
. Polynomials in 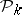 are called orthogonal polynomials for
are called orthogonal polynomials for  and
and 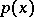 .
.
Theorem 4) There exists a cubature formula (1) possessing the 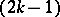 -property and having
-property and having 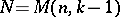 knots (the lower bound) if and only if the knots are the common roots of all orthogonal polynomials for
knots (the lower bound) if and only if the knots are the common roots of all orthogonal polynomials for  and
and 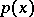 of degree
of degree 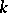 .
.
Theorem 5) If  orthogonal polynomials of degree
orthogonal polynomials of degree 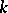 have
have 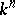 finite and pairwise distinct common roots, these roots can be chosen as knots for a cubature formula (1) possessing the
finite and pairwise distinct common roots, these roots can be chosen as knots for a cubature formula (1) possessing the 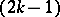 -property.
-property.
The error of a cubature formula (1) in which 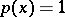 and
and  is bounded is defined by
is bounded is defined by
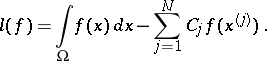 |
Let 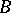 be a Banach space of functions such that
be a Banach space of functions such that 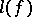 is a linear functional on
is a linear functional on 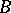 . The norm of the functional
. The norm of the functional 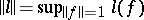 characterizes the quality of a given cubature formula for all functions of
characterizes the quality of a given cubature formula for all functions of 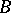 . Another approach to the construction of cubature formulas is based on minimizing
. Another approach to the construction of cubature formulas is based on minimizing  as a function of the knots and the coefficients of the (unknown) cubature formula (with only the number of knots fixed). Implementation of this approach, however, involves difficulties even for
as a function of the knots and the coefficients of the (unknown) cubature formula (with only the number of knots fixed). Implementation of this approach, however, involves difficulties even for 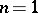 . Important results for any
. Important results for any 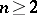 have been obtained by S.L. Sobolev [4]. The question of minimizing
have been obtained by S.L. Sobolev [4]. The question of minimizing  as a function of the coefficients for a given set of knots has been solved completely; the problem of choosing the knots is based on the assumption that they form a parallelepipedal grid and that the minimization depends exclusively on the parameters of this grid. The space
as a function of the coefficients for a given set of knots has been solved completely; the problem of choosing the knots is based on the assumption that they form a parallelepipedal grid and that the minimization depends exclusively on the parameters of this grid. The space 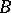 , in particular, may be
, in particular, may be 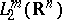 , where
, where  , and in that case the desired cubature formula is assumed to be exact for all polynomials of degree at most
, and in that case the desired cubature formula is assumed to be exact for all polynomials of degree at most 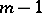 .
.
References
| [1] | N.M. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian) |
| [2] | V.I. Krylov, L.T. Shul'gina, "Handbook on numerical integration" , Moscow (1966) (In Russian) |
| [3] | A.H. Stroud, "Approximate calculation of multiple integrals" , Prentice-Hall (1971) |
| [4] | S.L. Sobolev, "Introduction to the theory of cubature formulas" , Moscow (1974) (In Russian) |
| [5] | S.L. Sobolev, "Formulas for mechanical cubature on the surface of a sphere" Sibirsk. Mat. Zh. , 3 : 5 (1962) pp. 769–796 (In Russian) |
| [6] | I.P. Mysovskikh, "Interpolatory cubature formulas" , Moscow (1981) (In Russian) |
Comments
The polynomial 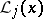 "of the influence of the j-th knot" (i.e. defined by
"of the influence of the j-th knot" (i.e. defined by 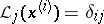 ) is also called the basic Lagrangian (for
) is also called the basic Lagrangian (for 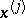 ).
).
The "m-property" is also known in Western literature as the degree of precision; i.e. a cubature formula has the 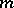 -property if it has degree of precision
-property if it has degree of precision 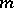 .
.
Reference [a1] is both an excellent introduction as well as an advanced treatment of cubature formulas.
References
| [a1] | H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980) |
| [a2] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984) |
Cubature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cubature_formula&oldid=19012