Complete instability
A property of a dynamical system. A dynamical system is called completely unstable if all its points are wandering points (cf. Wandering point).
For a dynamical system given in 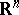 to be globally straightenable (or globally rectifiable) (i.e. there exists a topological imbedding
to be globally straightenable (or globally rectifiable) (i.e. there exists a topological imbedding 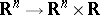 that maps each trajectory of the system into some straight line
that maps each trajectory of the system into some straight line 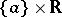 , where the point
, where the point  depends on the trajectory) it is necessary and sufficient that it is completely unstable and has no saddle at infinity (Nemytskii's theorem [1]).
depends on the trajectory) it is necessary and sufficient that it is completely unstable and has no saddle at infinity (Nemytskii's theorem [1]).
References
| [1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
Comments
For a slightly different formulation of Nemytskii's theorem (avoiding the notion of saddle at infinity), see [a2]. An easily accessible proof is given in [a1]. The property of being globally straightenable is closely related to that of being globally parallelizable: A dynamical system is said to be (globally) parallelizable whenever it is isomorphic to a system of the form  where all points move with speed 1 along the lines
where all points move with speed 1 along the lines 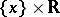 (
(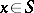 ).
).
References
| [a1] | J. Dugundji, H.A. Antosiewicz, "Parallelizable flows and Liapunov's second method" Ann. of Math. , 73 (1961) pp. 543–555 |
| [a2] | V.V. Nemytskii, "Topological problems in the theory of dynamical systems" AMS Transl. Series 1 , 5 (1954) pp. 414–497 Uspekhi Mat. Nauk , 4 (1949) pp. 91–153 |
Complete instability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_instability&oldid=12672