Commutator subgroup
of a group, derived group, second term of the lower central series, of a group
The subgroup of the group 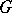 generated by all commutators of the elements of
generated by all commutators of the elements of 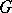 (cf. Commutator). The commutator subgroup of
(cf. Commutator). The commutator subgroup of 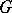 is usually denoted by
is usually denoted by 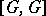 ,
, 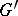 or
or 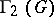 . The commutator subgroup is a fully-characteristic subgroup, and any subgroup containing the commutator subgroup is a normal subgroup. The quotient group with respect to some normal subgroup is Abelian if and only if this normal subgroup contains the commutator subgroup of the group.
. The commutator subgroup is a fully-characteristic subgroup, and any subgroup containing the commutator subgroup is a normal subgroup. The quotient group with respect to some normal subgroup is Abelian if and only if this normal subgroup contains the commutator subgroup of the group.
The commutator ideal of a ring 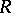 is the ideal generated by all products
is the ideal generated by all products 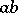 ,
, 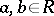 ; it is also called the square of
; it is also called the square of 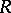 and is denoted by
and is denoted by 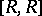 or
or 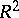 .
.
Both the above concepts are special cases of the notion of the commutator subgroup of a multi-operator  -group
-group 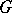 , which is defined as the ideal generated by all commutators and all elements of the form
, which is defined as the ideal generated by all commutators and all elements of the form
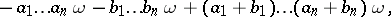 | (*) |
where 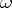 is an
is an  -ary operation in
-ary operation in  and
and
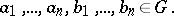 |
Comments
In the case of a ring considered as an operator  -group the commutators (of the underlying commutative group) are all zero, so that the commutator ideal is the ideal generated by all elements
-group the commutators (of the underlying commutative group) are all zero, so that the commutator ideal is the ideal generated by all elements 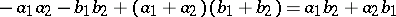 . Hence
. Hence 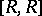 is the ideal generated by all products
is the ideal generated by all products 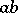 .
.
More generally, in all three cases one defines the commutator group (ideal) 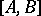 of two
of two  -subgroups
-subgroups 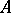 and
and 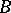 as the ideal generated by all commutators
as the ideal generated by all commutators 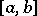 ,
, 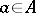 ,
, 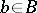 , and all elements (*) with
, and all elements (*) with 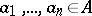 ,
, 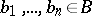 .
.
In the case of a ring 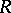 there is a second, different notion which also goes by the name of commutator ideal. It is the ideal generated by all commutators
there is a second, different notion which also goes by the name of commutator ideal. It is the ideal generated by all commutators 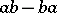 ,
, 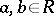 . This one is universal for homomorphisms of
. This one is universal for homomorphisms of 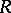 into commutative rings. I.e. if
into commutative rings. I.e. if  is this ideal and
is this ideal and 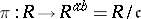 is the natural projection, then for each homomorphism
is the natural projection, then for each homomorphism 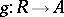 into a commutative ring
into a commutative ring 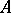 there is a unique homomorphism
there is a unique homomorphism 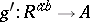 such that
such that 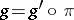 (
(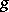 factors uniquely through
factors uniquely through 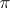 ). This is analogous to the property that for ordinary groups
). This is analogous to the property that for ordinary groups 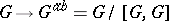 is universal for mappings of
is universal for mappings of 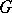 into Abelian groups (cf. Universal problems).
into Abelian groups (cf. Universal problems).
References
| [a1] | P.M. Cohn, "Algebra" , 2 , Wiley (1977) |
| [a2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Commutator subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commutator_subgroup&oldid=13613