Closure of a computational algorithm
A system of equations
 | (1) |
obtained as the limit as  ,
,  of a system of partially solved equations
of a system of partially solved equations
 | (2) |
describing the successive steps of a computational algorithm for the solution of an equation
 | (3) |
(for example, a finite-difference equation, in which case 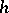 is the grid spacing), which approximates the equation
is the grid spacing), which approximates the equation
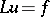 | (4) |
as  . It is assumed here that
. It is assumed here that 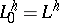 ,
,  ,
,  is the identity operator, and that
is the identity operator, and that  , i.e. the
, i.e. the 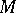 -th step of the algorithm yields a final solution of the approximate equation (3). The function
-th step of the algorithm yields a final solution of the approximate equation (3). The function  is assumed to increase with
is assumed to increase with 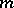 (e.g. is a linearly increasing function) and to satisfy the boundary conditions
(e.g. is a linearly increasing function) and to satisfy the boundary conditions 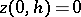 ,
, 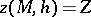 . The case
. The case 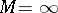 is admissible; then
is admissible; then 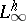 ,
, 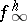 ,
, 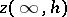 are interpreted as the limits of the variables
are interpreted as the limits of the variables 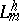 ,
, 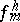 ,
, 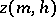 as
as 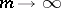 . The case
. The case 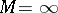 corresponds to iteration methods for solving equation (3).
corresponds to iteration methods for solving equation (3).
If the operators  in equation (1) are uniformly bounded in
in equation (1) are uniformly bounded in  , one says that algorithm (2) admits a regular closure. Although the set of algorithms with regular closure does not coincide with the set of actually stable algorithms, construction of a closed algorithm frequently helps in investigating the stability of an algorithm under various perturbations (in particular computational errors) (see [3], [4]).
, one says that algorithm (2) admits a regular closure. Although the set of algorithms with regular closure does not coincide with the set of actually stable algorithms, construction of a closed algorithm frequently helps in investigating the stability of an algorithm under various perturbations (in particular computational errors) (see [3], [4]).
The concept of a closed algorithm was introduced in [1]. There the closure of an algorithm for successive elimination of unknowns, when solving finite-difference equations that approximate an equation (4) with 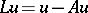 , where
, where 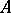 is a Fredholm integral operator, was obtained and investigated.
is a Fredholm integral operator, was obtained and investigated.
The construction of the closure of an algorithm and the inverse operation — the construction of a discrete algorithm the closure of which is a given continuous process — proves useful in designing new methods for the solution of problems. In particular, a large number of iteration methods admit closures which are steady processes. For example, the simple iteration method for the solution of the Laplace difference equation corresponds to the steady process 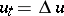 ; and the two-step iteration method corresponds to the steady process
; and the two-step iteration method corresponds to the steady process 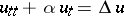 ,
,  (see [5]).
(see [5]).
References
| [1] | S.L. Sobolev, "Some remarks on the numerical solution of integral equations" Izv. Akad. Nauk SSSR Ser. Mat. , 20 : 4 (1956) pp. 413–436 (In Russian) |
| [2] | I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Closure of computational processes and the double-sweep method" Zh. Vychisl. Mat. i Mat. Fiz. , 4 : 2 (1964) pp. 351–353 (In Russian) |
| [3] | N.S. Bakhalov, "Computational methods for the solution of ordinary differential equations" , Kiev (1970) (In Russian) |
| [4] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [5] | V.K. Saul'ev, "Integration of equations of parabolic type by the method of nets" , Pergamon (1964) (Translated from Russian) |
| [6] | A.F. Shapkin, "Closure of two computational algorithms, based on the idea of orthogonalization" Zh. Vychisl. Mat. i Mat. Fiz. , 7 : 2 (1967) pp. 411–416 (In Russian) |
Comments
References
| [a1] | I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Numerical processes in differential equations" , Wiley (1966) |
Closure of a computational algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closure_of_a_computational_algorithm&oldid=17866