Classical group

The group of automorphisms of some sesquilinear form 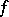on a right 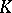-module 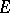, where 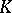is a ring; here 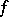and (and 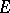sometimes 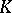as well) usually satisfy extra conditions. There is no precise definition of a classical group. It is supposed that 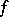is either the null form or is a non-degenerate reflexive form; sometimes 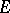is taken to be a free module of finite type. Often one means by classical groups other groups closely related to groups of automorphisms of forms (for example, their commutator subgroups or quotients with respect to the centre) or some of their extensions (for example, groups of semi-linear transformations of preserving 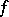up to a scalar factor and an automorphism of ).

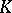Classical groups are closely related to geometry: They can be characterized as groups of those transformations of projective spaces (and also of certain varieties related to Grassmannians, see [2]) that preserve the natural incidence relations. For example, according to the fundamental theorem of projective geometry, the group of all transformations of -dimensional projective space 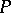over a skew-field 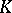that preserve collinearity coincides for 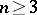with the classical group of all projective collineations of 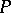. For this reason, the study of the structure of a classical group has a geometrical meaning; it is equivalent to the study of the symmetries (automorphisms) of the corresponding geometry.

The theory of classical groups has been developed most profoundly for the case when 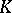is a skew-field and 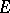is a vector space of finite dimension over 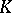. From now on, these conditions will be assumed to hold. Then the groups of the following series (to be described below) are usually called classical: , , , , .

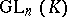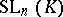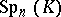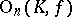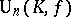1) Let 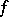be the null form. Then the group of all automorphisms of 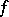is the same as the group of all automorphisms of 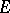(that is, bijective linear mappings from into 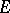); it is denoted by 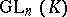and is called the general linear group in variables over the skew-field 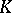, sometimes the full linear group. The subgroup of generated by all transvections (cf. Transvection) is denoted by 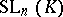and is called the special linear group (or unimodular group) in variables over the skew-field 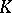. It is the same as the set of automorphisms with determinant .

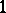2) Let 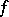be a non-degenerate sesquilinear form (with respect to an involution 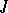of 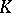) for which the orthogonality relation is symmetric, that is

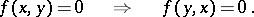Such a form is called reflexive. The group 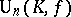of all automorphisms of 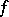is called the unitary group in variables over the skew-field 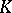with respect to the form 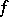. There are only two possibilities: Either 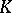is a field, 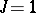and 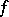is a skew-symmetric bilinear form, or by multiplying 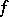by a suitable scalar and altering 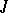, one can arrange for 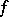to be a Hermitian or skew-Hermitian form. For a skew-symmetric form 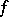, 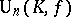is called the symplectic group in variables over the skew-field 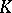(if 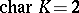one must suppose that 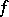is an alternating form); it is denoted by 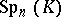. This notation does not include 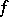because all non-degenerate alternating forms on 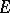are equivalent and define isomorphic symplectic groups. In this case is even. For Hermitian and skew-Hermitian forms, there is the special case that 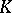is a field of characteristic different from 2, 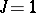and 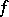is a symmetric bilinear form. Then 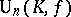is called the orthogonal group in variables over the field 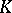with respect to the form 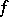; it is denoted by 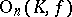. Orthogonal groups can also be defined for fields of characteristic 2 (see [2]). Often the term "unitary group" is used in a narrower sense for groups 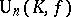that are neither orthogonal nor symplectic, that is, groups corresponding to non-trivial involutions .

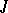Associated with each of the fundamental series of classical groups are their projective images 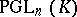, , 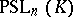, , 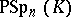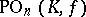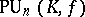; these are the quotient groups of them by the intersections with the centre 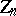of 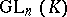. The group

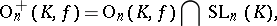the commutator subgroup 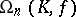of 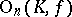, the group

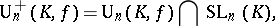and their projective images are also associated with the series of orthogonal and unitary classical groups, respectively.

The classical approach to the theory of classical groups aims at the elucidation of their algebraic structure. This reduces to the description of a normal series of subgroups and their successive quotient groups (in particular a description of normal subgroups and simple composition factors), the description of the automorphisms and isomorphisms of the classical groups (and, more generally, of the homomorphisms), the description of the various types of generating sets and their relations, etc. The main results on the structure of groups of type 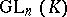and 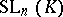are the following. The commutator subgroup of 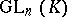, , 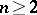is 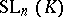, except in the case 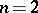, 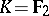(where 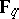is the field of 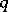elements). The centre 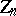of 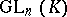consists of all homotheties 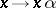, where 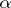is an element of the centre of 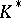. There is a normal series of subgroups

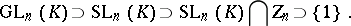The group 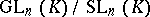is isomorphic to 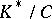, where 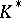is the multiplicative group of the skew-field and 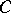is its commutator subgroup. The group 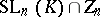is the centre of 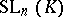and the quotient group

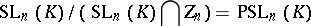is simple in all cases except when 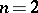, 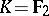or 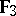. For further details see General linear group; Special linear group; Symplectic group; Orthogonal group; Unitary group. The structure of a classical group depends essentially on its type, the skew-field 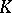, the properties of the form 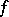, and . For some types of classical groups a very detailed description is available. For others there are still open questions. (These involve mainly groups of type 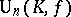where 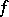is an anisotropic form.) Typical for the structure theory of classical groups are assertions that hold for almost-all 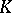, 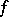and , and the investigation of the various exceptional cases when these assertions are false. 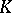(Such exceptions arise for instance for small values of , for finite fields of small order or for special values of the index of the form .)

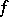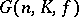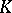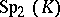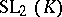The question of isomorphisms of classical groups occupies a special position. First there are the standard isomorphisms. These are isomorphisms between and the definition of which does not depend on special properties of (except, perhaps, its commutativity). All other isomorphisms are called non-standard. 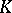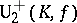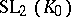For example, there is a (standard) isomorphism from onto , where is any field, or from onto , where 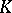is any field, 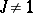, 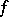is a form of index 1, and 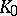is the field of invariants of 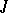. For a detailed description of the known standard isomorphisms, see [2], [3]. Examples of non-standard isomorphisms are:

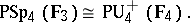It is also known that the groups 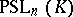and 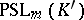, , 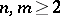can be isomorphic only when 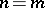, apart from the case

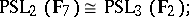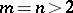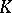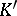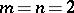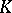when , isomorphism is possible only if and are isomorphic or anti-isomorphic; this is also the case when if and 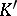are fields, apart from the case

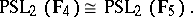The groups 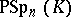and 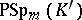can be isomorphic only if 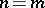and 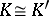, apart from the case 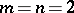, , 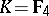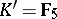. There are no other isomorphisms among the groups 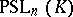, , 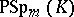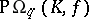(where 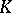is a finite field) apart from the ones indicated above.

The results listed above on the structure of classical groups and their isomorphisms are obtained by methods of linear algebra and projective geometry. The basis for this consists in the study of special elements in the classical groups and the geometric properties of them, principally the study of transvections, involutions and planar rotations. Subsequently, methods of the theory of Lie groups and algebraic geometry were introduced into the theory of classical groups, whereupon the theory of classical groups became much related with the general theory of semi-simple linear algebraic groups in which classical groups appear as forms (cf. Form of an algebraic group): Every form of a simple linear algebraic group over a field 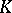of classical type (that is, of type 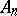, , 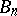, 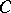or 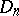) gives rise to a classical group, the group of its 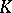-rational points (an exception being a form of 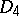connected with an outer automorphism of order three). 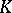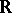In the case when is or 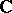, a classical group is naturally endowed with a Lie group structure, and for 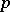-adic fields with a 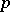-adic analytic group structure. This makes it possible to use topological methods in the study of such classical groups, and conversely, to obtain information on the topological structure of the underlying variety of a classical group (for example, on its finite cellular decompositions) from the knowledge of its algebraic structure.

In the more general situation when 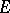is a module over a ring 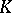the results on classical groups are not so exhaustive (see [3]). Here the theory of classical groups links up with algebraic 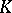-theory.

References

[1]	E. Artin, "Geometric algebra" , Interscience (1957)
[2]	J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955)
[3]	A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966)
[4]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French)

Comments

Instead of [3] one may consult [a1], [a2], [a3].

References

[a1]	A. Borel, J. Tits, "Homomorphisms "abstraits" de groupes algébriques simples" Ann. of Math. (2) , 97 (1973) pp. 499–571
[a2]	O.T. O'Meara, "A survey of the isomorphism theory of the classical groups" , Ring theory and algebra , 3 , M. Dekker (1980) pp. 225–242
[a3]	A. Weil, "Algebras with involutions and the classical groups" J. Ind. Math. Soc. , 24 (1960) pp. 589–623