Carleman formulas
Let 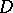 be a bounded domain in
be a bounded domain in  with piecewise smooth boundary
with piecewise smooth boundary 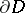 , and let
, and let 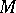 be a set of positive
be a set of positive 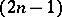 -dimensional Lebesgue measure in
-dimensional Lebesgue measure in 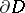 .
.
The following boundary value problem can then be posed (cf. also Boundary value problems of analytic function theory): Given a holomorphic function 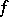 in
in 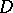 that is sufficiently well-behaved up to the boundary
that is sufficiently well-behaved up to the boundary 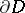 (for example,
(for example, 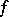 is continuous in
is continuous in 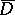 ,
, 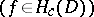 , or
, or  belongs to the Hardy class
belongs to the Hardy class 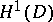 ) how can it be reconstructed inside
) how can it be reconstructed inside 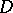 by its values on
by its values on 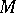 by means of an integral formula?
by means of an integral formula?
Three methods of solution are known, due to:
1) Carleman–Goluzin–Krylov;
2) M.M. Lavrent'ev; and
3) A.M. Kytmanov. See [a1].
The following are some very simple solutions:
a) 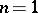 . If
. If 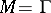 is a smooth arc connecting two points of the unit circle
is a smooth arc connecting two points of the unit circle 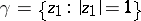 and lying inside
and lying inside 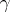 and
and 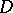 is the domain bounded by a part of
is the domain bounded by a part of 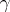 and the arc
and the arc 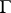 , with
, with 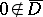 , then for
, then for 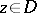 and
and 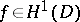 the following Carleman formula holds:
the following Carleman formula holds:
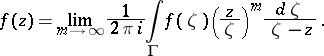 |
b)  . Let
. Let  be a circular convex bounded domain (a Cartan domain) with
be a circular convex bounded domain (a Cartan domain) with 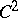 -boundary and let
-boundary and let 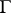 be a piecewise smooth hypersurface intersecting
be a piecewise smooth hypersurface intersecting  and cutting from it the domain
and cutting from it the domain 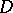 , with
, with 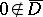 . Then there exists a Cauchy–Fantappié formula for the domain
. Then there exists a Cauchy–Fantappié formula for the domain 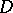 with kernel holomorphic in
with kernel holomorphic in  . Let
. Let 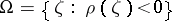 ,
, 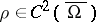 , and
, and 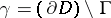 . Assume that there exists a vector-valued function (a "barrier" )
. Assume that there exists a vector-valued function (a "barrier" ) 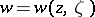 ,
, 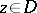 ,
, 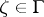 , such that
, such that 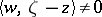 ,
, 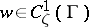 , and
, and 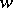 smoothly extends to
smoothly extends to 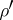 on
on 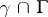 , where
, where 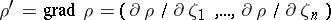 . Then for every function
. Then for every function  and
and  , the following Carleman formula with holomorphic kernel is valid (see [a2]):
, the following Carleman formula with holomorphic kernel is valid (see [a2]):
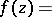 |
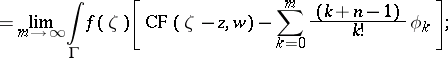 |
here, 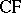 is the Cauchy–Fantappié differential form (see [a3])
is the Cauchy–Fantappié differential form (see [a3])
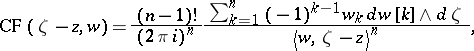 |
where 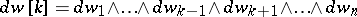 ,
, 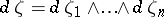 ,
, 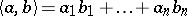 ,
,
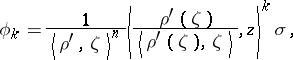 |
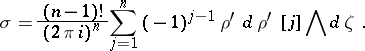 |
c) Now, let  be an
be an  -circular domain (a Reinhardt domain); then
-circular domain (a Reinhardt domain); then
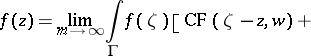 |
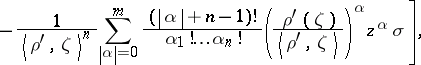 |
where 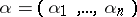 , all
, all 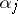 are non-negative integers,
are non-negative integers, 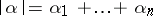 ,
, 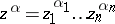 .
.
If 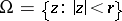 is a ball, then
is a ball, then
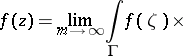 |
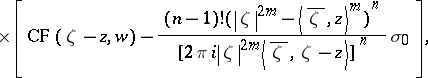 |
where
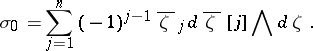 |
In all the above Carleman formulas the limits are understood in the sense of uniform convergence on compact subsets of  . A description of the class of holomorphic functions representable by Carleman formulas is given in [a4]. In [a1] applications of Carleman formulas in analysis and in mathematical physics can be found as well.
. A description of the class of holomorphic functions representable by Carleman formulas is given in [a4]. In [a1] applications of Carleman formulas in analysis and in mathematical physics can be found as well.
References
| [a1] | L. Aizenberg, "Carleman's formulas in complex analysis" , Kluwer Acad. Publ. (1993) |
| [a2] | L. Aizenberg, "Carleman's formulas and conditions of analytic extendability" , Topics in Complex Analysis , Banach Centre Publ. , 31 , Banach Centre (1995) pp. 27–34 |
| [a3] | L. Aizenberg, A.P. Yuzhakov, "Integral representation and residues in multidimensional complex analysis" , Amer. Math. Soc. (1983) (In Russian) |
| [a4] | L. Aizenberg, A. Tumanov, A. Vidras, "The class of holomorphic functions representable by Carleman formula" Ann. Scuola Norm. Pisa , 27 : 1 (1998) pp. 93–105 |
Carleman formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleman_formulas&oldid=16201