Borel set
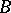 -set
-set
A set which may be obtained as the result of not more than a countable number of operations of union and intersection of closed and open sets in a topological space. More exactly, a Borel set is an element of the smallest countably-additive class of sets containing the closed sets, and which is closed with respect to complementation. Borel sets are also called Borel-measurable sets and 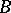 -measurable sets. Open and closed sets are said to be Borel sets of order zero. Borel sets of order one are sets of type
-measurable sets. Open and closed sets are said to be Borel sets of order zero. Borel sets of order one are sets of type  or
or 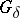 which are, respectively, countable sums of closed sets and countable intersections of open sets. Borel sets of the second order are sets of type
which are, respectively, countable sums of closed sets and countable intersections of open sets. Borel sets of the second order are sets of type 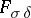 (the intersection of a countable number of sets of type
(the intersection of a countable number of sets of type 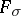 ) and sets of type
) and sets of type 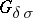 (the union of a countable number of sets of type
(the union of a countable number of sets of type 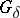 ). Borel sets of an arbitrary finite order are defined in a similar manner by induction. With the aid of transfinite numbers of the second class (cf. Transfinite number) this classification may be exhaustively extended to all Borel sets. Let
). Borel sets of an arbitrary finite order are defined in a similar manner by induction. With the aid of transfinite numbers of the second class (cf. Transfinite number) this classification may be exhaustively extended to all Borel sets. Let 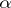 be an arbitrary transfinite number of the second class; the Borel sets of class
be an arbitrary transfinite number of the second class; the Borel sets of class 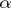 will include any Borel set of order
will include any Borel set of order  that is not a Borel set of order
that is not a Borel set of order 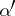 for any
for any 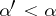 . Whether the classes of Borel sets are empty or not will depend on the basic space under consideration. In Euclidean, Hilbert and Baire spaces there exist Borel sets of all classes.
. Whether the classes of Borel sets are empty or not will depend on the basic space under consideration. In Euclidean, Hilbert and Baire spaces there exist Borel sets of all classes.
Borel sets are a special case of 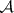 -sets. For an
-sets. For an 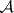 -set
-set 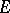 to be a Borel set it is necessary and sufficient that the complement of
to be a Borel set it is necessary and sufficient that the complement of 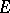 also is an
also is an 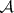 -set (Suslin's criterion). In spaces with a Lebesgue measure all Borel sets are Lebesgue measurable. The converse proposition is not true. All separable spaces having the cardinality of the continuum contain sets that are not Borel sets.
-set (Suslin's criterion). In spaces with a Lebesgue measure all Borel sets are Lebesgue measurable. The converse proposition is not true. All separable spaces having the cardinality of the continuum contain sets that are not Borel sets.
Borel sets were introduced by E. Borel [1]; they play an important role in the study of Borel functions (cf. Borel function).
In a more general sense a Borel set is a set in an arbitrary Borel system of sets generated by some system of sets. The Borel sets in a topological space are generated by the system of closed subsets of this space.
References
| [1] | E. Borel, "Leçons sur les fonctions discontinues" , Gauthier-Villars (1898) |
| [2] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) |
| [3] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [4] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
For notational questions, see Borel set of ambiguous class.
References
| [a1] | K. Kuratowski, "Introduction to set theory and topology" , Pergamon (1961) (Translated from Polish) |
Borel set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_set&oldid=15948