Bootstrap method
A computer-intensive "resampling" method, introduced in statistics by B. Efron in 1979 [a3] for estimating the variability of statistical quantities and for setting confidence regions (cf. also Sample; Confidence set). The name "bootstrap" refers to the analogy with pulling oneself up by one's own bootstraps. Efron's bootstrap is to resample the data. Given observations  , artificial bootstrap samples are drawn with replacement from
, artificial bootstrap samples are drawn with replacement from 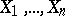 , putting equal probability mass
, putting equal probability mass 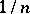 at each
at each 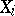 . For example, with sample size
. For example, with sample size  and distinct observations
and distinct observations 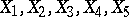 one might obtain
one might obtain 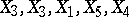 as bootstrap (re)sample. In fact, there are
as bootstrap (re)sample. In fact, there are  distinct bootstrap samples in this case.
distinct bootstrap samples in this case.
A more formal description of Efron's non-parametric bootstrap in a simple setting is as follows. Suppose 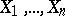 is a random sample of size
is a random sample of size  from a population with unknown distribution function
from a population with unknown distribution function 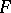 on the real line; i.e. the
on the real line; i.e. the 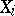 's are assumed to be independent and identically distributed random variables with common distribution function
's are assumed to be independent and identically distributed random variables with common distribution function 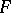 (cf. also Random variable). Let
(cf. also Random variable). Let 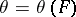 denote a real-valued parameter to be estimated. Let
denote a real-valued parameter to be estimated. Let 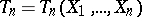 denote an estimate of
denote an estimate of 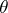 , based on the data
, based on the data 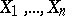 (cf. also Statistical estimation; Statistical estimator). The object of interest is the probability distribution
(cf. also Statistical estimation; Statistical estimator). The object of interest is the probability distribution 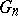 of
of 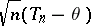 ; i.e.
; i.e.
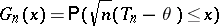 |
for all real  , the exact distribution function of
, the exact distribution function of  , properly normalized. The scaling factor
, properly normalized. The scaling factor  is a classical one, while the centring of
is a classical one, while the centring of  is by the parameter
is by the parameter 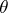 . Here
. Here 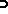 denotes "probability" corresponding to
denotes "probability" corresponding to 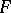 .
.
Efron's non-parametric bootstrap estimator of 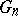 is now given by
is now given by
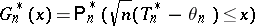 |
for all real  . Here
. Here 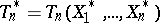 , where
, where 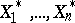 denotes an artificial random sample (the bootstrap sample) from
denotes an artificial random sample (the bootstrap sample) from 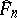 , the empirical distribution function of the original observations
, the empirical distribution function of the original observations 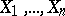 , and
, and 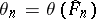 . Note that
. Note that 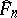 is the random distribution (a step function) which puts probability mass
is the random distribution (a step function) which puts probability mass 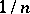 at each of the
at each of the  's (
's (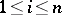 ), sometimes referred to as the resampling distribution;
), sometimes referred to as the resampling distribution; 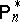 denotes "probability" corresponding to
denotes "probability" corresponding to 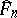 , conditionally given
, conditionally given  , i.e. given the observations
, i.e. given the observations 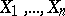 . Obviously, given the observed values
. Obviously, given the observed values  in the sample,
in the sample, 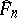 is completely known and (at least in principle)
is completely known and (at least in principle) 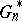 is also completely known. One may view
is also completely known. One may view 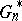 as the empirical counterpart in the "bootstrap world" to
as the empirical counterpart in the "bootstrap world" to 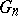 in the "real world" . In practice, exact computation of
in the "real world" . In practice, exact computation of 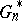 is usually impossible (for a sample
is usually impossible (for a sample 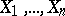 of
of  distinct numbers there are
distinct numbers there are 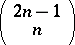 distinct bootstrap (re)samples), but
distinct bootstrap (re)samples), but 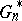 can be approximated by means of Monte-Carlo simulation (cf. also Monte-Carlo method). Efficient bootstrap simulation is discussed e.g. in [a2], [a10].
can be approximated by means of Monte-Carlo simulation (cf. also Monte-Carlo method). Efficient bootstrap simulation is discussed e.g. in [a2], [a10].
When does Efron's bootstrap work? The consistency of the bootstrap approximation 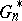 , viewed as an estimate of
, viewed as an estimate of 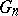 , i.e. one requires
, i.e. one requires
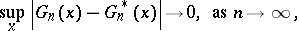 |
to hold, in 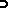 -probability, is generally viewed as an absolute prerequisite for Efron's bootstrap to work in the problem at hand. Of course, bootstrap consistency is only a first-order asymptotic result and the error committed when
-probability, is generally viewed as an absolute prerequisite for Efron's bootstrap to work in the problem at hand. Of course, bootstrap consistency is only a first-order asymptotic result and the error committed when 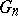 is estimated by
is estimated by 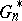 may still be quite large in finite samples. Second-order asymptotics (Edgeworth expansions; cf. also Edgeworth series) enables one to investigate the speed at which
may still be quite large in finite samples. Second-order asymptotics (Edgeworth expansions; cf. also Edgeworth series) enables one to investigate the speed at which 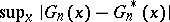 approaches zero, and also to identify cases where the rate of convergence is faster than
approaches zero, and also to identify cases where the rate of convergence is faster than 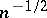 , the classical Berry–Esseen-type rate for the normal approximation. An example in which the bootstrap possesses the beneficial property of being more accurate than the traditional normal approximation is the Student
, the classical Berry–Esseen-type rate for the normal approximation. An example in which the bootstrap possesses the beneficial property of being more accurate than the traditional normal approximation is the Student 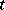 -statistic and more generally Studentized statistics. For this reason the use of bootstrapped Studentized statistics for setting confidence intervals is strongly advocated in a number of important problems. A general reference is [a7].
-statistic and more generally Studentized statistics. For this reason the use of bootstrapped Studentized statistics for setting confidence intervals is strongly advocated in a number of important problems. A general reference is [a7].
When does the bootstrap fail? It has been proved [a1] that in the case of the mean, Efron's bootstrap fails when 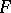 is the domain of attraction of an
is the domain of attraction of an 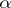 -stable law with
-stable law with 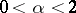 (cf. also Attraction domain of a stable distribution). However, by resampling from
(cf. also Attraction domain of a stable distribution). However, by resampling from 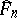 , with (smaller) resample size
, with (smaller) resample size 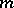 , satisfying
, satisfying 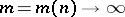 and
and  , it can be shown that the (modified) bootstrap works. More generally, in recent years the importance of a proper choice of the resampling distribution has become clear, see e.g. [a5], [a9], [a10].
, it can be shown that the (modified) bootstrap works. More generally, in recent years the importance of a proper choice of the resampling distribution has become clear, see e.g. [a5], [a9], [a10].
The bootstrap can be an effective tool in many problems of statistical inference; e.g. the construction of a confidence band in non-parametric regression, testing for the number of modes of a density, or the calibration of confidence bounds, see e.g. [a2], [a4], [a8]. Resampling methods for dependent data, such as the "block bootstrap" , is another important topic of recent research, see e.g. [a2], [a6].
References
| [a1] | K.B. Athreya, "Bootstrap of the mean in the infinite variance case" Ann. Statist. , 15 (1987) pp. 724–731 |
| [a2] | A.C. Davison, D.V. Hinkley, "Bootstrap methods and their application" , Cambridge Univ. Press (1997) |
| [a3] | B. Efron, "Bootstrap methods: another look at the jackknife" Ann. Statist. , 7 (1979) pp. 1–26 |
| [a4] | B. Efron, R.J. Tibshirani, "An introduction to the bootstrap" , Chapman&Hall (1993) |
| [a5] | E. Giné, "Lectures on some aspects of the bootstrap" P. Bernard (ed.) , Ecole d'Eté de Probab. Saint Flour XXVI-1996 , Lecture Notes Math. , 1665 , Springer (1997) |
| [a6] | F. Götze, H.R. Künsch, "Second order correctness of the blockwise bootstrap for stationary observations" Ann. Statist. , 24 (1996) pp. 1914–1933 |
| [a7] | P. Hall, "The bootstrap and Edgeworth expansion" , Springer (1992) |
| [a8] | E. Mammen, "When does bootstrap work? Asymptotic results and simulations" , Lecture Notes Statist. , 77 , Springer (1992) |
| [a9] | H. Putter, W.R. van Zwet, "Resampling: consistency of substitution estimators" Ann. Statist. , 24 (1996) pp. 2297–2318 |
| [a10] | J. Shao, D. Tu, "The jackknife and bootstrap" , Springer (1995) |
Bootstrap method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bootstrap_method&oldid=11753