Approximation of a differential operator by difference operators
An approximation of the differential operator by parameter-dependent operators such that the result of their application to a function is determined by the values of this function on some discrete set of points — a grid — which become more exact as its parameter (mesh, step of the grid) tends to zero.
Let 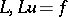 , be a differential operator which converts any function
, be a differential operator which converts any function  of a class of functions
of a class of functions 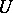 into a function
into a function 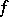 of a linear normed space
of a linear normed space 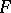 . Let
. Let 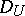 be the domain of definition of the functions in
be the domain of definition of the functions in 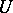 , and let there be some discrete subset in
, and let there be some discrete subset in 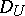 — a grid
— a grid 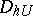 — which "becomes more dense" as
— which "becomes more dense" as 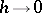 . Consider the set
. Consider the set 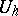 of all functions
of all functions 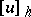 defined on the grid only and coinciding with
defined on the grid only and coinciding with  in the points of the grid. A difference operator is defined as any operator
in the points of the grid. A difference operator is defined as any operator 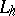 that converts the grid functions in
that converts the grid functions in 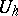 into functions
into functions 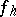 in
in 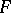 . One says that the operator
. One says that the operator  ,
, 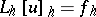 , represents an order
, represents an order 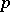 approximation to the differential operator
approximation to the differential operator 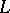 on
on  if for any function
if for any function 
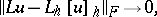 |
 |
as  . Occasionally, an approximation is understood to be the equality
. Occasionally, an approximation is understood to be the equality
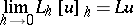 |
in the sense of some weak convergence. The approximation of a differential operator by difference operators is used for an approximate computation of the function 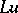 from the table of values
from the table of values 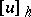 of the function
of the function  and for the approximation of a differential equation by difference equations.
and for the approximation of a differential equation by difference equations.
There are two principal methods for constructing operators 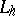 approximating
approximating 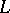 .
.
In the first method  is defined as the result of applying the differential operator
is defined as the result of applying the differential operator 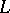 to a function in
to a function in 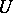 , obtained by some interpolation formula from the grid function
, obtained by some interpolation formula from the grid function 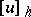 .
.
The second method is as follows. In the domain 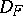 of definition of a function
of definition of a function  in
in 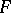 one introduces a grid
one introduces a grid 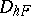 , and considers the linear space
, and considers the linear space 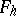 of grid functions defined on
of grid functions defined on 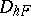 . The operator
. The operator  is constructed as the product of two operators: an operator which converts the function
is constructed as the product of two operators: an operator which converts the function 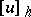 into the grid function
into the grid function 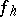 in
in 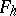 , i.e. into a table of approximate values of
, i.e. into a table of approximate values of  , and an operator which extends
, and an operator which extends 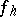 from
from 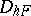 to the entire domain
to the entire domain 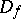 . For instance, in order to approximate the differential operator
. For instance, in order to approximate the differential operator
 |
one constructs the grid 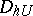 consisting of points
consisting of points 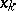 ,
,  ,
,
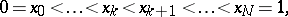 |
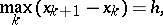 |
and a grid 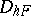 consisting of the points
consisting of the points
 |
 |
The values of the operator 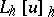 at the points
at the points 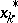 are defined by the equations:
are defined by the equations:
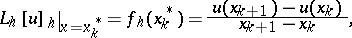 |
 |
Thereafter, the definition of  is piecewise linearly extended outside
is piecewise linearly extended outside  with possible breaks at the points
with possible breaks at the points 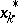 ,
, 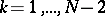 , only.
, only.
Let the norm in F be defined by the formula
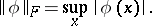 |
Then, on the class of functions 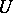 with a bounded third derivative, for
with a bounded third derivative, for 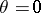 and
and 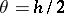 the operator
the operator  represents an order 1, respectively 2, approximation to
represents an order 1, respectively 2, approximation to  . On the class
. On the class 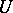 of functions with bounded second derivatives, the representation is of order 1 only, for any
of functions with bounded second derivatives, the representation is of order 1 only, for any 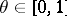 .
.
The task of approximating a differential operator by finite-difference operators is sometimes conditionally considered as solved if a method is found for the construction of the grid function
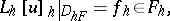 |
determined at the points of 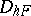 only, while the task of completing the function
only, while the task of completing the function 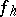 everywhere on
everywhere on 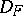 is ignored. In such a case the approximation is defined by considering the space
is ignored. In such a case the approximation is defined by considering the space 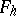 as normed, and by assuming, for the grid and for the norm, that for any function
as normed, and by assuming, for the grid and for the norm, that for any function 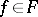 , the function
, the function 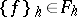 , which coincides with
, which coincides with  at the points of
at the points of 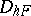 , satisfies the equation
, satisfies the equation
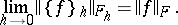 |
The operator 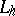 is understood to be an operator from
is understood to be an operator from 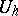 in
in  , and one says that
, and one says that 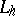 represents an order
represents an order 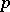 approximation to
approximation to  on
on 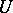 if, for
if, for 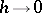 ,
,
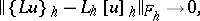 |
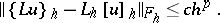 |
In order to construct an operator 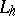 which is an approximation to
which is an approximation to 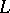 of given order on sufficiently smooth functions, one often replaces each derivative contained in the expression
of given order on sufficiently smooth functions, one often replaces each derivative contained in the expression 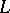 by its finite-difference approximation, basing oneself on the following fact. For any integers
by its finite-difference approximation, basing oneself on the following fact. For any integers 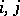 and for any
and for any 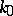 ,
,  , in the equation
, in the equation
 |
it is possible, by using the method of undetermined coefficients and Taylor's formula, to select numbers 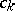 not depending on
not depending on 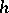 , so that for any function
, so that for any function 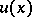 with
with 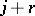 (
(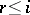 ) bounded derivatives, an inequality of the type
) bounded derivatives, an inequality of the type
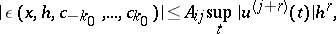 |
where 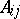 depends only on
depends only on 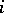 and
and 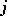 , is valid. As an example, suppose one constructs an approximating operator for the Laplace operator
, is valid. As an example, suppose one constructs an approximating operator for the Laplace operator 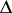 ,
,
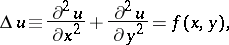 |
if 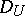 is the closed square
is the closed square 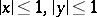 , and
, and 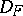 is its interior
is its interior 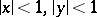 . Assume that
. Assume that 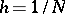 where
where 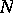 is a natural number, and construct the grid with points
is a natural number, and construct the grid with points
 |
which belong to  . The points
. The points
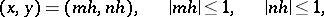 |
then belong to 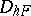 , for integers
, for integers 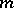 and
and  . Since
. Since
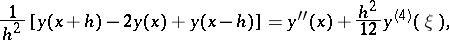 |
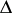 can be approximated with second-order accuracy on a space of sufficiently smooth functions by the finite-difference operator
can be approximated with second-order accuracy on a space of sufficiently smooth functions by the finite-difference operator  if one puts, at the points of
if one puts, at the points of 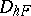 :
:
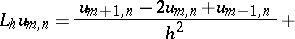 |
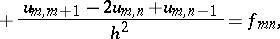 |
where  and
and 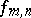 are the values of the functions
are the values of the functions 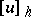 and
and 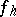 at the point
at the point 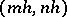 .
.
There are also other methods of constructing operators 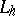 which are approximations to the operator
which are approximations to the operator 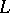 on the space of solutions
on the space of solutions  of the differential equation
of the differential equation  , and which satisfy additional conditions.
, and which satisfy additional conditions.
References
| [1] | A.F. Filippov, "On stability of difference equations" Dokl. Akad. Nauk SSSR , 100 : 6 (1955) pp. 1045–1048 (In Russian) |
| [2] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
Comments
The approximation of a differential operator by difference operators is an ingredient for both the approximation of a differential equation by difference equations and for the approximation of a differential boundary value problem by difference boundary value problems, and is therefore extensively treated in the literature on (finite-) difference methods for ordinary and partial differential equations. The references listed below not only provide discretizations of differential equations and boundary value problems, but also the solution of these problems. References [a1]–[a3], [a5], [a6] are introducing textbooks, whereas [a4], [a7], [a8] and [a9] also present more advanced material.
References
| [a1] | W.F. Ames, "Numerical methods for partial differential equations" , Nelson , London (1969) |
| [a2] | G.E. Forsythe, W.R. Wasow, "Finite difference methods for partial differential equations" , Wiley (1960) |
| [a3] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a4] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
| [a5] | J.D. Lambert, "Computational methods in ordinary differential equations" , Wiley (1973) |
| [a6] | A.R. Mitchell, D.F. Griffiths, "The finite difference method in partial differential equations" , Wiley (1980) |
| [a7] | R.D. Richtmeyer, K.W. Morton, "Difference methods for initial value problems" , Wiley (1967) |
| [a8] | A.A. Samarskii, "Theorie der Differenzverfahren" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1984) (Translated from Russian) |
| [a9] | H.J. Stetter, "Analysis of discretization methods for ordinary differential equations" , Springer (1973) |
Approximation of a differential operator by difference operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_of_a_differential_operator_by_difference_operators&oldid=16233