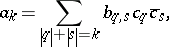|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| − | The following classical assertion is well known. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202301.png" /> be a simply connected bounded domain with smooth boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202302.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202303.png" />. Then
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202304.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table>
| + | Out of 88 formulas, 86 were replaced by TEX code.--> |
| | | | |
| − | if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202305.png" /> extends into the domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202306.png" /> as a [[Holomorphic function|holomorphic function]] of the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202307.png" />. For the multi-dimensional case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202308.png" />, instead of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a1202309.png" />, one takes an exterior differential form of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023010.png" />.
| + | {{TEX|semi-auto}}{{TEX|part}} |
| | + | The following classical assertion is well known. Let $D \subset \mathbf{C}$ be a simply connected bounded domain with smooth boundary $\partial D$, and $f \in C ( \partial D )$. Then |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023011.png" /> is defined only on a part of the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023012.png" />, then the existence of an [[Analytic continuation|analytic continuation]] into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023013.png" /> cannot be decided by the vanishing of some family of continuous linear functionals as in (a1). Solutions to this problem were given from the 1950s onwards by many mathematicians, see, e.g. [[#References|[a1]]], [[#References|[a2]]].
| + | \begin{equation} \tag{a1} \int _ { \partial D } f z _ { 1 } ^ { m } d z _ { 1 } = 0 , \quad m = 0,1 , \dots , \end{equation} |
| | + | |
| | + | if and only if $f ( z )$ extends into the domain $D$ as a [[Holomorphic function|holomorphic function]] of the class $H ( D ) \cap C ( \overline { D } )$. For the multi-dimensional case $D \subset \mathbf{C} ^ { x }$, instead of the form $z _ { 1 } ^ { m } d z _ { 1 }$, one takes an exterior differential form of class $Z _ { n , n - 1 } ^ { \infty } ( \overline { D } )$. |
| | + | |
| | + | If $f$ is defined only on a part of the boundary of $D$, then the existence of an [[Analytic continuation|analytic continuation]] into $D$ cannot be decided by the vanishing of some family of continuous linear functionals as in (a1). Solutions to this problem were given from the 1950s onwards by many mathematicians, see, e.g. [[#References|[a1]]], [[#References|[a2]]]. |
| | | | |
| | Some very simple solutions are given below. | | Some very simple solutions are given below. |
| | | | |
| − | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023014.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023015.png" /> be the domain bounded by a part of the unit circle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023016.png" /> and a smooth open arc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023017.png" /> connecting two points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023018.png" /> and lying inside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023019.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023020.png" />. Set | + | 1) $n = 1$. Let $D$ be the domain bounded by a part of the unit circle $\gamma = \{ z _ { 1 } : | z _ { 1 } | = 1 \}$ and a smooth open arc $\Gamma$ connecting two points of $\gamma$ and lying inside $\gamma$. Let $0 \notin \overline { D }$. Set |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023021.png" /></td> </tr></table>
| + | \begin{equation*} a _ { k } = \int _ { \Gamma } \frac { f ( \zeta ) d \zeta } { \zeta ^ { k + 1 } } , \quad k = 0,1, \dots . \end{equation*} |
| | | | |
| − | Then the following assertion holds: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023022.png" />, then there is a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023023.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023024.png" /> if and only if | + | Then the following assertion holds: If $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$, then there is a function $F \in H ( D ) \cap C ( D \cup \Gamma )$ such that $F | _ { \Gamma } = f$ if and only if |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023025.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table>
| + | \begin{equation} \tag{a2} \operatorname { limsup } _ { k \rightarrow \infty } \sqrt [ | a _k |] {k}\leq 1 \end{equation} |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023026.png" /> is not identically zero, then (a2) is equivalent to | + | If $f | _ { \Gamma }$ is not identically zero, then (a2) is equivalent to |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023027.png" /></td> </tr></table>
| + | \begin{equation*} \limsup _ { k \rightarrow \infty } \sqrt [ |a_{ k } | ] { k } = 1. \end{equation*} |
| | | | |
| − | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023028.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023029.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023031.png" />-circular convex domain in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023033.png" /> are natural numbers, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023034.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023035.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023036.png" />. In particular, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023037.png" /> this circular domain is a Cartan domain. Moreover, assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023038.png" /> is convex and bounded and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023039.png" />. Furthermore, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023040.png" /> be the domain bounded by a part of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023041.png" /> and a hyper-surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023042.png" /> dividing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023043.png" /> into two parts and assume that the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023044.png" /> contains the origin. Consider the Cauchy–Fantappié differential form | + | 2) $n > 1$. Let $\Omega = \{ \zeta : \psi ( \zeta ) < 0 \}$ be a $( p _ { 1 } , \dots , p _ { n } )$-circular convex domain in $\mathbf{C} ^ { n }$, where $p _ { 1 } , \dots , p _ { n }$ are natural numbers, i.e., $z \in \Omega$ implies $( z _ { 1 } e ^ { i t p _ { 1 } } 1 , \ldots , z _ { n } e ^ { i t p _ { n } } ) \in \Omega$ for $t \in \mathbf{R}$. In particular, for $p _ { 1 } = \ldots = p _ { n } = 1$ this circular domain is a Cartan domain. Moreover, assume that $\Omega$ is convex and bounded and $\partial \Omega \in C ^ { 2 }$. Furthermore, let $D$ be the domain bounded by a part of $\partial \Omega$ and a hyper-surface $\Gamma \in C ^ { 2 }$ dividing $\Omega$ into two parts and assume that the complement of $\overline{ D }$ contains the origin. Consider the Cauchy–Fantappié differential form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023045.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{CF} ( \zeta - z , w ) = \frac { ( n - 1 ) ! \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } w _ { k } d w [ k ] \wedge d \zeta } { \langle w , \zeta - z \rangle ^ { n } }, \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023048.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023049.png" />. By the Sard theorem, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023050.png" /> for almost all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023051.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023052.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023053.png" /> is the homothetic transform of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023054.png" />. Assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023055.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023056.png" /> and set | + | where $d w [ k ] = d w _ { 1 } \wedge \ldots \wedge d w _ { k - 1 } \wedge d w _ { k + 1 } \wedge \ldots \wedge d w _ { n }$, $d \zeta = d \zeta _ { 1 } \wedge \ldots \wedge d \zeta _ { n }$, $\langle a , b \rangle = a _ { 1 } b _ { 1 } + \ldots + a _ { n } b _ { n }$. Then $\operatorname { grad } \psi = ( \partial \psi / \partial \zeta _ { 1 } , \dots , \partial \psi / \partial \zeta _ { n } )$. By the Sard theorem, $\operatorname{grad} \psi \neq 0$ for almost all $r$ on $\partial \Omega _ { r }$, where $\Omega _ { r } = r \Omega$ is the homothetic transform of $\Omega$. Assume that $\operatorname{grad} \psi \neq 0$ on $\Gamma$ and set |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023057.png" /></td> </tr></table>
| + | \begin{equation*} c _ { q } = \frac { ( | q | + n - 1 ) ! } { q _ { 1 } ! \ldots q _ { n } ! } \times \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023058.png" /></td> </tr></table>
| + | \begin{equation*} \times \int _ { \Gamma } f ( \zeta ) \left( \frac { \operatorname { grad } \psi } { ( \operatorname { grad } \psi , \zeta ) } \right) ^ { q } \operatorname {CF} ( \zeta , \operatorname { grad } \psi ), \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023061.png" />. Let | + | where $q = ( q _ { 1 } , \dots , q _ { n } )$, $| q | = q _1 + \ldots + q_n$, $w ^ { q } = w _ { 1 } ^ { q _ { 1 } } \ldots w _ { n } ^ { q _ { n } }$. Let |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023062.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023062.png"/></td> </tr></table> |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023063.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023064.png" /> is the volume element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023065.png" />. Here, all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023067.png" /> are non-negative integers. Note that the integral moments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023068.png" /> depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023070.png" />, but the moments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023071.png" /> depend only on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023072.png" />. | + | where $b _ { q , s } = \int _{\Omega} z ^{q} \overline{z} ^ { s } d v$ and $d v$ is the volume element in $\Omega$. Here, all $q_j$ and $s _ { j }$ are non-negative integers. Note that the integral moments $c _ { q }$ depend on $f$ and $\Gamma$, but the moments $b _ { q ,\, s }$ depend only on $\Omega$. |
| | | | |
| − | The following assertion now holds: For a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023073.png" /> to have an analytic continuation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023074.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023075.png" />, it is necessary and sufficient that the following two conditions are fulfilled: | + | The following assertion now holds: For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation $F \in H ( D ) \cap C ( D \cup \Gamma )$ with $F | _ { \Gamma } = f$, it is necessary and sufficient that the following two conditions are fulfilled: |
| | | | |
| − | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023076.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023078.png" />-function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023079.png" />; | + | i) $f$ is a $C R$-function on $\Gamma$; |
| | | | |
| − | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023080.png" />. | + | ii) $\limsup_{k \rightarrow \infty} \sqrt [ a _ { k } ] { k } \leq 1$. |
| | | | |
| − | A consequence of this is as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023081.png" /> be a bounded convex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023082.png" />-circular domain (a Reinhardt domain). Set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023083.png" />. For a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023084.png" /> to have an analytic continuation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023085.png" /> as above it is necessary and sufficient that: | + | A consequence of this is as follows. Let $\Omega \subset {\bf C} ^ { n }$ be a bounded convex $n$-circular domain (a Reinhardt domain). Set $d _ { q } ( \Omega ) = \operatorname { max } _ { \overline{\Omega} } | z ^ { q } |$. For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation in $D$ as above it is necessary and sufficient that: |
| | | | |
| − | a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023086.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023087.png" />-function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023088.png" />; | + | a) $f$ is a $C R$-function on $\Gamma$; |
| | | | |
| − | b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120230/a12023089.png" />. | + | b) $\operatorname { lim}\operatorname { sup}_{| q | \rightarrow \infty} \sqrt[ |c _ { q } | d _ { q } ( \Omega ) ] { | q | } \leq 1$. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Aizenberg, "Carleman's formulas in complex analysis" , Kluwer Acad. Publ. (1993)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Aizenberg, "Carleman's formulas and conditions of analytic extendability" , ''Topics in Complex Analysis'' , ''Banach Centre Publ.'' , '''31''' , Banach Centre (1995) pp. 27–34</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L. Aizenberg, "Carleman's formulas in complex analysis" , Kluwer Acad. Publ. (1993)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L. Aizenberg, "Carleman's formulas and conditions of analytic extendability" , ''Topics in Complex Analysis'' , ''Banach Centre Publ.'' , '''31''' , Banach Centre (1995) pp. 27–34</td></tr></table> |
The following classical assertion is well known. Let $D \subset \mathbf{C}$ be a simply connected bounded domain with smooth boundary $\partial D$, and $f \in C ( \partial D )$. Then
\begin{equation} \tag{a1} \int _ { \partial D } f z _ { 1 } ^ { m } d z _ { 1 } = 0 , \quad m = 0,1 , \dots , \end{equation}
if and only if $f ( z )$ extends into the domain $D$ as a holomorphic function of the class $H ( D ) \cap C ( \overline { D } )$. For the multi-dimensional case $D \subset \mathbf{C} ^ { x }$, instead of the form $z _ { 1 } ^ { m } d z _ { 1 }$, one takes an exterior differential form of class $Z _ { n , n - 1 } ^ { \infty } ( \overline { D } )$.
If $f$ is defined only on a part of the boundary of $D$, then the existence of an analytic continuation into $D$ cannot be decided by the vanishing of some family of continuous linear functionals as in (a1). Solutions to this problem were given from the 1950s onwards by many mathematicians, see, e.g. [a1], [a2].
Some very simple solutions are given below.
1) $n = 1$. Let $D$ be the domain bounded by a part of the unit circle $\gamma = \{ z _ { 1 } : | z _ { 1 } | = 1 \}$ and a smooth open arc $\Gamma$ connecting two points of $\gamma$ and lying inside $\gamma$. Let $0 \notin \overline { D }$. Set
\begin{equation*} a _ { k } = \int _ { \Gamma } \frac { f ( \zeta ) d \zeta } { \zeta ^ { k + 1 } } , \quad k = 0,1, \dots . \end{equation*}
Then the following assertion holds: If $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$, then there is a function $F \in H ( D ) \cap C ( D \cup \Gamma )$ such that $F | _ { \Gamma } = f$ if and only if
\begin{equation} \tag{a2} \operatorname { limsup } _ { k \rightarrow \infty } \sqrt [ | a _k |] {k}\leq 1 \end{equation}
If $f | _ { \Gamma }$ is not identically zero, then (a2) is equivalent to
\begin{equation*} \limsup _ { k \rightarrow \infty } \sqrt [ |a_{ k } | ] { k } = 1. \end{equation*}
2) $n > 1$. Let $\Omega = \{ \zeta : \psi ( \zeta ) < 0 \}$ be a $( p _ { 1 } , \dots , p _ { n } )$-circular convex domain in $\mathbf{C} ^ { n }$, where $p _ { 1 } , \dots , p _ { n }$ are natural numbers, i.e., $z \in \Omega$ implies $( z _ { 1 } e ^ { i t p _ { 1 } } 1 , \ldots , z _ { n } e ^ { i t p _ { n } } ) \in \Omega$ for $t \in \mathbf{R}$. In particular, for $p _ { 1 } = \ldots = p _ { n } = 1$ this circular domain is a Cartan domain. Moreover, assume that $\Omega$ is convex and bounded and $\partial \Omega \in C ^ { 2 }$. Furthermore, let $D$ be the domain bounded by a part of $\partial \Omega$ and a hyper-surface $\Gamma \in C ^ { 2 }$ dividing $\Omega$ into two parts and assume that the complement of $\overline{ D }$ contains the origin. Consider the Cauchy–Fantappié differential form
\begin{equation*} \operatorname{CF} ( \zeta - z , w ) = \frac { ( n - 1 ) ! \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } w _ { k } d w [ k ] \wedge d \zeta } { \langle w , \zeta - z \rangle ^ { n } }, \end{equation*}
where $d w [ k ] = d w _ { 1 } \wedge \ldots \wedge d w _ { k - 1 } \wedge d w _ { k + 1 } \wedge \ldots \wedge d w _ { n }$, $d \zeta = d \zeta _ { 1 } \wedge \ldots \wedge d \zeta _ { n }$, $\langle a , b \rangle = a _ { 1 } b _ { 1 } + \ldots + a _ { n } b _ { n }$. Then $\operatorname { grad } \psi = ( \partial \psi / \partial \zeta _ { 1 } , \dots , \partial \psi / \partial \zeta _ { n } )$. By the Sard theorem, $\operatorname{grad} \psi \neq 0$ for almost all $r$ on $\partial \Omega _ { r }$, where $\Omega _ { r } = r \Omega$ is the homothetic transform of $\Omega$. Assume that $\operatorname{grad} \psi \neq 0$ on $\Gamma$ and set
\begin{equation*} c _ { q } = \frac { ( | q | + n - 1 ) ! } { q _ { 1 } ! \ldots q _ { n } ! } \times \end{equation*}
\begin{equation*} \times \int _ { \Gamma } f ( \zeta ) \left( \frac { \operatorname { grad } \psi } { ( \operatorname { grad } \psi , \zeta ) } \right) ^ { q } \operatorname {CF} ( \zeta , \operatorname { grad } \psi ), \end{equation*}
where $q = ( q _ { 1 } , \dots , q _ { n } )$, $| q | = q _1 + \ldots + q_n$, $w ^ { q } = w _ { 1 } ^ { q _ { 1 } } \ldots w _ { n } ^ { q _ { n } }$. Let
where $b _ { q , s } = \int _{\Omega} z ^{q} \overline{z} ^ { s } d v$ and $d v$ is the volume element in $\Omega$. Here, all $q_j$ and $s _ { j }$ are non-negative integers. Note that the integral moments $c _ { q }$ depend on $f$ and $\Gamma$, but the moments $b _ { q ,\, s }$ depend only on $\Omega$.
The following assertion now holds: For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation $F \in H ( D ) \cap C ( D \cup \Gamma )$ with $F | _ { \Gamma } = f$, it is necessary and sufficient that the following two conditions are fulfilled:
i) $f$ is a $C R$-function on $\Gamma$;
ii) $\limsup_{k \rightarrow \infty} \sqrt [ a _ { k } ] { k } \leq 1$.
A consequence of this is as follows. Let $\Omega \subset {\bf C} ^ { n }$ be a bounded convex $n$-circular domain (a Reinhardt domain). Set $d _ { q } ( \Omega ) = \operatorname { max } _ { \overline{\Omega} } | z ^ { q } |$. For a function $f \in C ( \Gamma ) \cap L ^ { 1 } ( \Gamma )$ to have an analytic continuation in $D$ as above it is necessary and sufficient that:
a) $f$ is a $C R$-function on $\Gamma$;
b) $\operatorname { lim}\operatorname { sup}_{| q | \rightarrow \infty} \sqrt[ |c _ { q } | d _ { q } ( \Omega ) ] { | q | } \leq 1$.
References
| [a1] | L. Aizenberg, "Carleman's formulas in complex analysis" , Kluwer Acad. Publ. (1993) |
| [a2] | L. Aizenberg, "Carleman's formulas and conditions of analytic extendability" , Topics in Complex Analysis , Banach Centre Publ. , 31 , Banach Centre (1995) pp. 27–34 |