White noise
A generalized stationary stochastic process  with constant spectral density. The generalized correlation function of white noise has the form
with constant spectral density. The generalized correlation function of white noise has the form  , where
, where  is a positive constant and
is a positive constant and  is the delta-function. The white noise process is extensively applied in describing random disturbances with a very small correlation period (e.g. "thermal noisethermal noise" — pulsations of the current intensity in a conductor, generated by the thermal motion of the electrons). In the spectral decomposition of white noise,
is the delta-function. The white noise process is extensively applied in describing random disturbances with a very small correlation period (e.g. "thermal noisethermal noise" — pulsations of the current intensity in a conductor, generated by the thermal motion of the electrons). In the spectral decomposition of white noise,
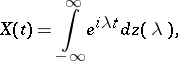 |
the "elementary vibrations"  have, on the average, the same intensity at all frequencies
have, on the average, the same intensity at all frequencies  ; more accurately, their average squared amplitude is
; more accurately, their average squared amplitude is
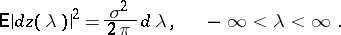 |
This spectral decomposition means that, for each square-integrable function  ,
,
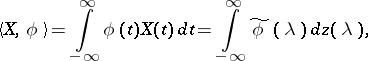 |
where  is the Fourier transform of
is the Fourier transform of  ; a more explicit dependence of the generalized process
; a more explicit dependence of the generalized process  on the function
on the function  may be described by a corresponding stochastic measure
may be described by a corresponding stochastic measure 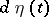 of the same type as
of the same type as  (
( is the Fourier transform of the stochastic measure
is the Fourier transform of the stochastic measure 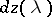 ), viz.
), viz.
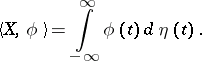 |
Gaussian white noise  , which is the generalized derivative of Brownian motion
, which is the generalized derivative of Brownian motion  (
( ), is the basis for constructing stochastic diffusion processes
), is the basis for constructing stochastic diffusion processes 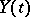 (cf. Diffusion process), "controllable" by a stochastic differential equation:
(cf. Diffusion process), "controllable" by a stochastic differential equation:
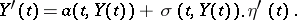 |
These equations are often written in the form of differentials:
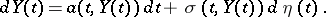 |
Another important model involving the use of white noise is the stochastic process  which describes the behaviour of a stable vibrating system acted upon by stationary random perturbations
which describes the behaviour of a stable vibrating system acted upon by stationary random perturbations  , when
, when  ,
, 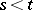 , do not depend on
, do not depend on  ,
,  . A very simple example of this is the system
. A very simple example of this is the system
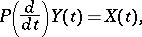 |
where  is a polynomial with roots in the left half-plane; after the damping of the "transient processes" , the process
is a polynomial with roots in the left half-plane; after the damping of the "transient processes" , the process  is given by
is given by
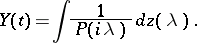 |
In practical applications, in the description of the so-called shot effect process, white noise of the form
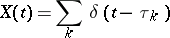 |
plays an important role ( varies between
varies between  and
and 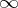 and the
and the 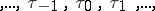 form a Poisson process); more accurately,
form a Poisson process); more accurately, 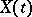 is the generalized derivative of a Poisson process
is the generalized derivative of a Poisson process  . The shot effect process itself has the form
. The shot effect process itself has the form
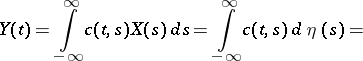 |
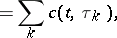 |
where  is some weight function satisfying the condition
is some weight function satisfying the condition
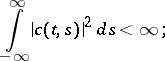 |
in addition, the average value of the generalized process 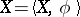 is
is
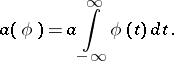 |
Here,  is the parameter of the Poisson law (see above), and the stochastic measure
is the parameter of the Poisson law (see above), and the stochastic measure 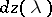 in the spectral representation
in the spectral representation
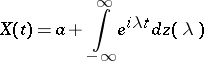 |
of this process is such that
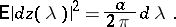 |
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
Comments
See [a1] for applications of white noise as the limit of "wide bandwidth" noise in physical systems and [a2] for the relationship between differential equations with white noise inputs and the stochastic differential equations of Itô calculus (cf. also Itô formula; Stochastic differential equation). See also Stratonovich integral for further information on this topic. Further important topics are the analysis of white noise regarded as a generalized random function [a3], i.e. a probability on the space  of tempered distributions on
of tempered distributions on  (cf. White noise analysis), and application of white noise theory in non-linear filtering [a4], where "white noise" is interpreted in terms of finitely-additive Gaussian measures on cylinder sets of a separable Hilbert space.
(cf. White noise analysis), and application of white noise theory in non-linear filtering [a4], where "white noise" is interpreted in terms of finitely-additive Gaussian measures on cylinder sets of a separable Hilbert space.
References
| [a1] | H.J. Kushner, "Approximation and weak convergence methods for random processes, with applications to stochastic systems theory" , M.I.T. (1984) |
| [a2] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland & Kodansha (1988) |
| [a3] | T. Hida, "Brownian motion" , Springer (1980) |
| [a4] | G. Kallianpur, R.L. Karandikar, "White noise theory of prediction, filtering and smoothing" , Gordon & Breach (1988) |
| [a5] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) pp. Chapt. III (Translated from Russian) |
| [a6] | T. Hida (ed.) H.-H. Kuo (ed.) J. Potthoff (ed.) L. Streid (ed.) , White noise analysis - mathematics and applications , World Sci. (1990) |
White noise. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=White_noise&oldid=19248