Cohomology ring

A ring the additive group of which is the graded cohomology group

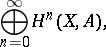where is a chain complex, is a coefficient group and the multiplication is defined by the linear set of mappings

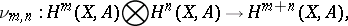for all , which are the inner cohomology multiplications (cup products). The cohomology ring turns out to be equipped with the structure of a graded ring.

For the existence of the mappings it is enough to have a set of mappings satisfying certain additional properties, and a mapping , that is, a multiplication in the coefficient group (see [2]). The induce mappings

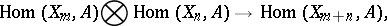which in their turn induce mappings 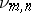in cohomology.

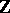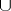In particular, a ring structure is defined on the graded group , where is a group and is the ring of integers with a trivial -action. The corresponding mappings coincide with the -product. This is an associative ring with identity, and for homogeneous elements 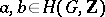of degrees respectively, .

Analogously, the -product defines a ring structure on the group , where is the -dimensional singular cohomology group of a topological space with coefficients in .

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[2]	S. MacLane, "Homology" , Springer (1963)

References

[a1]	A. Dold, "Lectures on algebraic topology" , Springer (1972) pp. Chapt. VII