Perfect compactification
A compactification  of a completely-regular space
of a completely-regular space  such that the closure in
such that the closure in  of the boundary of any open set
of the boundary of any open set  coincides with the boundary of
coincides with the boundary of  , where
, where  is the maximal open set in
is the maximal open set in  for which
for which  . Equivalent definitions are as follows:
. Equivalent definitions are as follows:
a)  for any pair of disjoint open sets
for any pair of disjoint open sets 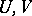 ;
;
b) if a closed set  partitions
partitions 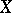 into open sets
into open sets  and
and 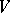 , then the closure of
, then the closure of  in
in 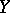 partitions
partitions  into
into  and
and 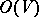 ;
;
c)  does not partition
does not partition 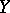 locally at any of its points.
locally at any of its points.
A compactification 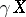 is perfect if and only if the natural mapping
is perfect if and only if the natural mapping 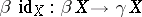 is monotone; here
is monotone; here 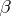 is the Stone–Čech compactification of
is the Stone–Čech compactification of  . Also,
. Also, 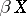 is the unique perfect compactification of
is the unique perfect compactification of 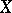 if and only if
if and only if 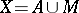 with
with  a compactum and
a compactum and 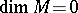 . The local connectedness of
. The local connectedness of 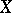 implies the local connectedness of any perfect extension
implies the local connectedness of any perfect extension 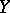 of
of 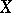 satisfying the first axiom of countability (and also the local connectedness of all intermediate extensions). Among all the perfect compactifications of
satisfying the first axiom of countability (and also the local connectedness of all intermediate extensions). Among all the perfect compactifications of  there is a minimal one,
there is a minimal one,  , if and only if
, if and only if  has at least one compactification with punctiform remainder (cf. Remainder of a space). The remainder in
has at least one compactification with punctiform remainder (cf. Remainder of a space). The remainder in  is punctiform and
is punctiform and  is the maximal such extension among those with punctiform remainder. Every homeomorphism of
is the maximal such extension among those with punctiform remainder. Every homeomorphism of 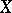 extends to a homeomorphism of
extends to a homeomorphism of  , and every perfect mapping from
, and every perfect mapping from 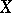 onto
onto  extends to a mapping from
extends to a mapping from 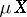 onto
onto 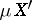 (provided
(provided 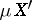 exists).
exists).
Comments
A space is called punctiform if and only if no compact connected subset contains more than one point.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) pp. 232ff (Translated from Russian) |
Perfect compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perfect_compactification&oldid=19245