Monomial
The simplest form of an algebraic expression, a polynomial containing only one term.
Like polynomials (see Ring of polynomials), monomials can be considered not only over a field but also over a ring. A monomial over a commutative ring  in a set of variables
in a set of variables  , where
, where  runs through some index set
runs through some index set  , is a pair
, is a pair  , where
, where  and
and  is a mapping of the set
is a mapping of the set  into the set of non-negative integers, where
into the set of non-negative integers, where  for all but a finite number of
for all but a finite number of  . A monomial is usually written in the form
. A monomial is usually written in the form
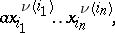 |
where 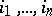 are all the indices for which
are all the indices for which  . The number
. The number  is called the degree of the monomial in the variable
is called the degree of the monomial in the variable  , and the sum
, and the sum 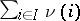 is called the total degree of the monomial. The elements of the ring can be regarded as monomials of degree 0. A monomial with
is called the total degree of the monomial. The elements of the ring can be regarded as monomials of degree 0. A monomial with  is called primitive. Any monomial with
is called primitive. Any monomial with 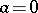 is identified with the element
is identified with the element  .
.
The set of monomials over  in the variables
in the variables  ,
,  , forms a commutative semi-group with identity. Here the product of two monomials
, forms a commutative semi-group with identity. Here the product of two monomials  and
and  is defined as
is defined as  .
.
Let  be a commutative
be a commutative  -algebra. Then the monomial
-algebra. Then the monomial  defines a mapping of
defines a mapping of 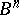 into
into  by the formula
by the formula  .
.
Monomials in non-commuting variables are sometimes considered. Such monomials are defined as expressions of the form
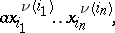 |
where the sequence of (not necessarily distinct) indices  is fixed.
is fixed.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
Monomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monomial&oldid=19244