Kernel of a summation method
A function  (depending on a parameter) the values of which are the averages of the given method of summation applied to the series
(depending on a parameter) the values of which are the averages of the given method of summation applied to the series
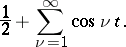 | (1) |
The kernel of a summation method gives an integral representation of the averages of the method in the summation of Fourier series. If the summation method is defined by a transformation of sequences into sequences using a matrix  , then the kernel of this method is the function
, then the kernel of this method is the function
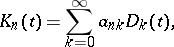 |
where  are the partial sums of the series (1):
are the partial sums of the series (1):
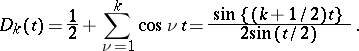 | (2) |
In this case the averages of the Fourier series for a  -periodic function
-periodic function  can be expressed in terms of
can be expressed in terms of  and the kernel by the formula
and the kernel by the formula
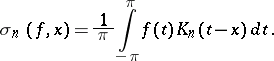 |
In particular, the kernel of the method of arithmetical averages (cf. Arithmetical averages, summation method of) has the form
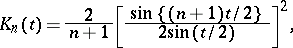 |
and is called the Fejér kernel. The kernel of the Abel summation method is given by
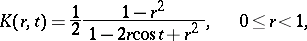 |
and is called the Poisson kernel. The function  in (2) is called the Dirichlet kernel.
in (2) is called the Dirichlet kernel.
The function 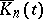 whose values are the averages of a summation method applied to the series
whose values are the averages of a summation method applied to the series
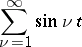 |
is called the conjugate kernel of the summation method.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
Kernel of a summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_a_summation_method&oldid=19229