Tensor algebra

A part of tensor calculus in which algebraic operations on tensors (cf. Tensor on a vector space) are studied.

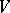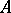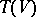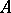The tensor algebra of a unitary module over a commutative associative ring with unit is the algebra over whose underlying module has the form

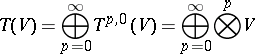and in which multiplication is defined with the help of tensor multiplication (cf. Tensor on a vector space). Besides the contravariant tensor algebra, the covariant tensor algebra

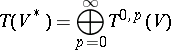is also considered, as well as the mixed tensor algebra

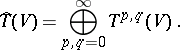If the module 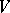is free and finitely generated, then 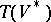is naturally isomorphic to the algebra of all multilinear forms (cf. Multilinear form) on 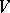. Any homomorphism of 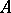-modules naturally defines a tensor algebra homomorphism .

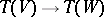The tensor algebra 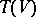is associative, but in general not commutative. Its unit is the unit of the ring 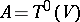. Any 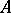-linear mapping of the module 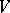into an associative 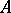-algebra 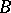with a unit can be naturally extended to a homomorphism of algebras 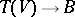mapping the unit to the unit. If 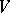is a free module with basis 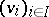, then 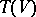is the free associative algebra with system of generators .

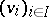References

[1]	N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French)
[2]	A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian)