Degenerate series of representations
The set of representations of a semi-simple Lie group 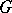 induced by the characters of a non-minimal parabolic subgroup
induced by the characters of a non-minimal parabolic subgroup 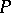 of it. Let
of it. Let 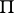 be a fundamental root system with respect to which the Lie algebra of a Borel subgroup
be a fundamental root system with respect to which the Lie algebra of a Borel subgroup 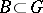 is spanned by the root vectors
is spanned by the root vectors 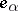 ,
, 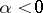 . The set of all parabolic subgroups containing
. The set of all parabolic subgroups containing  is in one-to-one correspondence with the set of all subsystems
is in one-to-one correspondence with the set of all subsystems 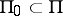 ;
; 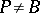 if
if 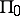 is non-empty, and the Lie algebra of the group
is non-empty, and the Lie algebra of the group 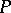 is generated by the
is generated by the 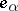 ,
, 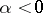 , and
, and 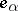 ,
, 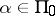 . Let
. Let 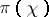 be the representation of the group
be the representation of the group 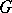 induced by a character
induced by a character 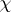 of
of 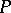 in the class
in the class 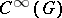 . There exist characters
. There exist characters 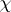 for which
for which 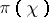 can be extended to a unitary representation of the group
can be extended to a unitary representation of the group 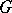 in
in  , where
, where 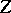 is a subgroup in
is a subgroup in 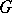 whose Lie algebra is spanned by the vectors
whose Lie algebra is spanned by the vectors 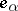 ,
, 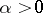 ,
,  ; here
; here 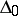 is the additive hull of
is the additive hull of 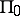 . Such representations are known as the representations of the basic degenerate series of representations. A supplementary degenerate series of representations is obtained by extending
. Such representations are known as the representations of the basic degenerate series of representations. A supplementary degenerate series of representations is obtained by extending 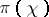 (for certain values of
(for certain values of 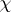 ) with respect to other scalar products in
) with respect to other scalar products in 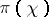 . The representations of a degenerate series of representations are irreducible for the group
. The representations of a degenerate series of representations are irreducible for the group 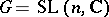 .
.
References
| [1] | I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian) |
| [2] | K.I. Gross, "The dual of a parabolic subgroup and a degenerate principal series of 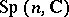 " Amer. J. Math. , 93 : 2 (1971) pp. 398–428 " Amer. J. Math. , 93 : 2 (1971) pp. 398–428 |
Comments
References
| [a1] | B. Speh, D.A., jr. Vogan, "Reducibility of general principal series representations" Acta Math. , 145 (1980) pp. 227–299 |
| [a2] | D.A., jr. Vogan, "The unitary dual of 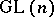 over an archimedean field" Invent. Math. , 83 (1986) pp. 449–505 over an archimedean field" Invent. Math. , 83 (1986) pp. 449–505 |
Degenerate series of representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_series_of_representations&oldid=19197