Elliptic coordinates
Two numbers  and
and  connected with rectangular Cartesian coordinates by the formulas
connected with rectangular Cartesian coordinates by the formulas
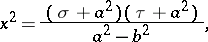 |
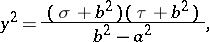 |
where  .
.

Figure: e035440a
The coordinate lines are (see Fig.): confocal ellipses ( ) and hyperbolas (
) and hyperbolas ( ) with foci (
) with foci ( ) and (
) and ( ). The system of elliptic coordinates is orthogonal. To every pair of numbers
). The system of elliptic coordinates is orthogonal. To every pair of numbers 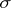 and
and  correspond four points, one in each quadrant of the
correspond four points, one in each quadrant of the 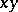 -plane.
-plane.
The Lamé coefficients are
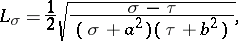 |
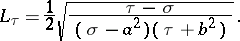 |
In elliptic coordinates the Laplace equation allows separation of variables.
Degenerate elliptic coordinates are two numbers 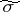 and
and 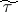 connected with
connected with  and
and  by the formulas (for
by the formulas (for 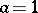 ,
, 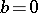 ):
):
 |
and with Cartesian coordinates  and
and 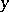 by
by
 |
where 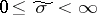 and
and 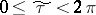 . Occasionally these coordinates are also called elliptic.
. Occasionally these coordinates are also called elliptic.
The Lamé coefficients are:
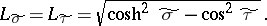 |
The area element is:
 |
The Laplace operator is:
 |
Comments
References
| [a1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) pp. 1–18 |
Elliptic coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_coordinates&oldid=19184