Integral surface
The surface in 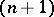 -dimensional space defined by an equation
-dimensional space defined by an equation 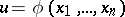 , where the function
, where the function 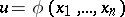 is a solution of a partial differential equation. For example, consider the linear homogeneous first-order equation
is a solution of a partial differential equation. For example, consider the linear homogeneous first-order equation
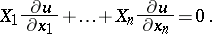 | (*) |
Here  is the unknown and
is the unknown and 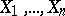 are given functions of the arguments
are given functions of the arguments  . Suppose that in some domain
. Suppose that in some domain 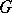 of
of  -dimensional space the functions
-dimensional space the functions 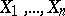 are continuously differentiable and do not vanish simultaneously, and suppose that the functions
are continuously differentiable and do not vanish simultaneously, and suppose that the functions 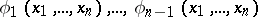 are functionally independent first integrals in
are functionally independent first integrals in 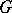 of the system of ordinary differential equations in symmetric form
of the system of ordinary differential equations in symmetric form
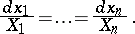 |
Then the equation of every integral surface of (*) in 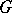 can be expressed in the form
can be expressed in the form
 |
where 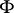 is a continuously-differentiable function. For a Pfaffian equation
is a continuously-differentiable function. For a Pfaffian equation
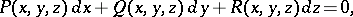 |
which is completely integrable in some domain 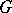 of three-dimensional space and does not have any singular points in
of three-dimensional space and does not have any singular points in 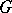 , each point of
, each point of 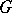 is contained in an integral surface. These integral surfaces never intersect nor are they tangent to one another at any point.
is contained in an integral surface. These integral surfaces never intersect nor are they tangent to one another at any point.
References
| [1] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
| [a2] | K. Rektorys (ed.) , Survey of applicable mathematics , Iliffe (1969) pp. Sect. 18.7 |
Integral surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_surface&oldid=19162