Irreducible matrix group
A group 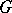 of
of 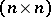 -matrices over a field
-matrices over a field 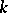 that cannot be brought by simultaneous conjugation in the general linear group
that cannot be brought by simultaneous conjugation in the general linear group 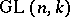 to the semi-reduced form
to the semi-reduced form
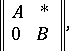 |
where 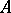 and
and 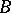 are square blocks of fixed dimensions. More accurately,
are square blocks of fixed dimensions. More accurately,  is called irreducible over the field
is called irreducible over the field 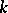 . In the language of transformations: A group
. In the language of transformations: A group 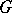 of linear transformations of a finite-dimensional vector space
of linear transformations of a finite-dimensional vector space 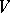 is called irreducible if
is called irreducible if 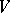 is a minimal
is a minimal 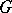 -invariant subspace (other than the null space). Irreducible Abelian groups of matrices over an algebraically closed field are one-dimensional. A group of matrices over a field that is irreducible over any extension field is called absolutely irreducible. If
-invariant subspace (other than the null space). Irreducible Abelian groups of matrices over an algebraically closed field are one-dimensional. A group of matrices over a field that is irreducible over any extension field is called absolutely irreducible. If 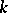 is algebraically closed, then for every group
is algebraically closed, then for every group 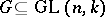 the following conditions are equivalent: 1)
the following conditions are equivalent: 1) 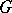 is irreducible over
is irreducible over 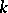 ; 2)
; 2) 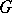 contains
contains 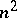 matrices that are linearly independent over
matrices that are linearly independent over 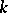 ; and 3)
; and 3) 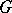 is absolutely irreducible. Thus, absolute irreducibility over a field
is absolutely irreducible. Thus, absolute irreducibility over a field 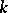 is equivalent to irreducibility over the algebraic closure of
is equivalent to irreducibility over the algebraic closure of 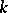 .
.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | Yu.I. Merzlyakov, "Rational groups" , Moscow (1987) (In Russian) |
Irreducible matrix group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irreducible_matrix_group&oldid=19107