Jacobian conjecture
Keller problem
Let 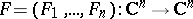 be a polynomial mapping, i.e. each
be a polynomial mapping, i.e. each 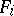 is a polynomial in
is a polynomial in  variables. If
variables. If 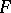 has a polynomial mapping as an inverse, then the chain rule implies that the determinant of the Jacobi matrix is a non-zero constant. In 1939, O.H. Keller asked: is the converse true?, i.e. does
has a polynomial mapping as an inverse, then the chain rule implies that the determinant of the Jacobi matrix is a non-zero constant. In 1939, O.H. Keller asked: is the converse true?, i.e. does 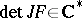 imply that
imply that 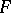 has a polynomial inverse?, [a4]. This problem is now known as Keller's problem but is more often called the Jacobian conjecture. This conjecture is still open (1999) for all
has a polynomial inverse?, [a4]. This problem is now known as Keller's problem but is more often called the Jacobian conjecture. This conjecture is still open (1999) for all 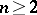 . Polynomial mappings satisfying
. Polynomial mappings satisfying  are called Keller mappings. Various special cases have been proved:
are called Keller mappings. Various special cases have been proved:
1) if 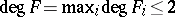 , the conjecture holds (S.S. Wang). Furthermore, it suffices to prove the conjecture for all
, the conjecture holds (S.S. Wang). Furthermore, it suffices to prove the conjecture for all 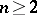 and all Keller mappings of the form
and all Keller mappings of the form 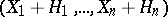 where each
where each 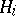 is either zero or homogeneous of degree
is either zero or homogeneous of degree  (H. Bass, E. Connell, D. Wright, A. Yagzhev). This case is referred to as the cubic homogeneous case. In fact, it even suffices to prove the conjecture for so-called cubic-linear mappings, i.e. cubic homogeneous mappings such that each
(H. Bass, E. Connell, D. Wright, A. Yagzhev). This case is referred to as the cubic homogeneous case. In fact, it even suffices to prove the conjecture for so-called cubic-linear mappings, i.e. cubic homogeneous mappings such that each 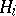 is of the form
is of the form 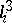 , where each
, where each  is a linear form (L. Drużkowski). The cubic homogeneous case has been verified for
is a linear form (L. Drużkowski). The cubic homogeneous case has been verified for  (
(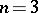 was settled by D. Wright;
was settled by D. Wright; 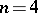 was settled by E. Hubbers).
was settled by E. Hubbers).
2) A necessary condition for the Jacobian conjecture to hold for all 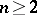 is that for Keller mappings of the form
is that for Keller mappings of the form 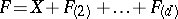 with all non-zero coefficients in each
with all non-zero coefficients in each 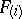 positive, the mapping
positive, the mapping 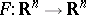 is injective (cf. also Injection), where
is injective (cf. also Injection), where  denotes the homogeneous part of degree
denotes the homogeneous part of degree 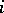 of
of 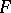 . It is known that this condition is also sufficient! (J. Yu). On the other hand, the Jacobian conjecture holds for all
. It is known that this condition is also sufficient! (J. Yu). On the other hand, the Jacobian conjecture holds for all 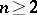 and all Keller mappings of the form
and all Keller mappings of the form 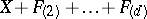 , where each non-zero coefficient of all
, where each non-zero coefficient of all 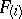 is negative (also J. Yu).
is negative (also J. Yu).
3) The Jacobian conjecture has been verified under various additional assumptions. Namely, if 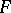 has a rational inverse (O.H. Keller) and, more generally, if the field extension
has a rational inverse (O.H. Keller) and, more generally, if the field extension 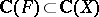 is a Galois extension (L.A. Campbell). Also, properness of
is a Galois extension (L.A. Campbell). Also, properness of 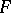 or, equivalently, if
or, equivalently, if 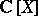 is finite over
is finite over 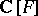 (cf. also Extension of a field) implies that a Keller mapping is invertible.
(cf. also Extension of a field) implies that a Keller mapping is invertible.
4) If  , the Jacobian conjecture has been verified for all Keller mappings
, the Jacobian conjecture has been verified for all Keller mappings 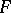 with
with  (T.T. Moh) and if
(T.T. Moh) and if 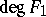 or
or  is a product of at most two prime numbers (H. Applegate, H. Onishi). Finally, if there exists one line
is a product of at most two prime numbers (H. Applegate, H. Onishi). Finally, if there exists one line  such that
such that 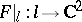 is injective, then a Keller mapping
is injective, then a Keller mapping 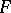 is invertible (J. Gwozdziewicz). There are various seemingly unrelated formulations of the Jacobian conjecture. For example,
is invertible (J. Gwozdziewicz). There are various seemingly unrelated formulations of the Jacobian conjecture. For example,
a) up to a polynomial coordinate change, 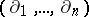 is the only commutative
is the only commutative 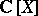 -basis of
-basis of 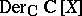 ;
;
b) every order-preserving 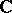 -endomorphism of the
-endomorphism of the  th Weyl algebra
th Weyl algebra 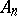 is an isomorphism (A. van den Essen).
is an isomorphism (A. van den Essen).
c) for every 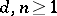 there exists a constant
there exists a constant 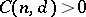 such that for every commutative
such that for every commutative 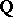 -algebra
-algebra 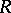 and every
and every  with
with 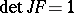 and
and 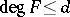 , one has
, one has 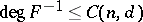 (H. Bass).
(H. Bass).
d) if  is a polynomial mapping such that
is a polynomial mapping such that  for some
for some 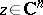 , then
, then  for some
for some 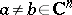 .
.
e) if, in the last formulation, one replaces 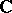 by
by 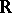 the so-called real Jacobian conjecture is obtained, i.e. if
the so-called real Jacobian conjecture is obtained, i.e. if 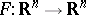 is a polynomial mapping such that
is a polynomial mapping such that 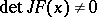 for all
for all  , then
, then 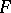 is injective. It was shown in 1994 (S. Pinchuk) that this conjecture is false for
is injective. It was shown in 1994 (S. Pinchuk) that this conjecture is false for 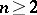 . Another conjecture, formulated by L. Markus and H. Yamabe in 1960 is the global asymptotic stability Jacobian conjecture, also called the Markus–Yamabe conjecture. It asserts that if
. Another conjecture, formulated by L. Markus and H. Yamabe in 1960 is the global asymptotic stability Jacobian conjecture, also called the Markus–Yamabe conjecture. It asserts that if 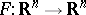 is a
is a 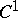 -mapping with
-mapping with 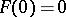 and such that for all
and such that for all  the real parts of all eigenvalues of
the real parts of all eigenvalues of  are
are 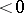 , then each solution of
, then each solution of 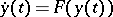 tends to zero if
tends to zero if 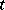 tends to infinity. The Markus–Yamabe conjecture (for all
tends to infinity. The Markus–Yamabe conjecture (for all  ) implies the Jacobian conjecture. For
) implies the Jacobian conjecture. For 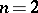 the Markus–Yamabe conjecture was proved to be true (R. Fessler, C. Gutierrez). However, in 1995 polynomial counterexamples where found for all
the Markus–Yamabe conjecture was proved to be true (R. Fessler, C. Gutierrez). However, in 1995 polynomial counterexamples where found for all 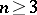 (A. Cima, A. van den Essen, A. Gasull, E. Hubbers, F. Mañosas).
(A. Cima, A. van den Essen, A. Gasull, E. Hubbers, F. Mañosas).
References
| [a1] | A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" J. Alev (ed.) et al. (ed.) , Algèbre Noncommutative, Groupes Quantiques et Invariants , SMF (1985) pp. 55–81 |
| [a2] | A. van den Essen, "Seven lectures on polynomial automorphisms" A. van den Essen (ed.) , Automorphisms of Affine Spaces , Kluwer Acad. Publ. (1995) pp. 3–39 |
| [a3] | H. Bass, E.H. Connell, D. Wright, "The Jacobian conjecture: reduction of degree and formal expansion of the inverse" Bull. Amer. Math. Soc. , 7 (1982) pp. 287–330 |
| [a4] | O.H. Keller, "Ganze Cremonatransformationen" Monatschr. Math. Phys. , 47 (1939) pp. 229–306 |
| [a5] | A. van den Essen, "Polynomial automorphisms and the Jacobian conjecture" , Birkhäuser (to appear in 2000) |
Jacobian conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobian_conjecture&oldid=19054