Bayesian estimator
An estimator of an unknown parameter from the results of observations using the Bayesian approach. In such an approach to the problem of statistical estimation it is usually assumed that the unknown parameter 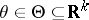 is a random variable with given a priori distribution
is a random variable with given a priori distribution 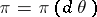 , that the space of decisions
, that the space of decisions 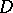 is identical to the set
is identical to the set 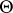 and that the loss
and that the loss 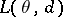 expresses the deviation between the variable
expresses the deviation between the variable 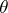 and its estimator
and its estimator 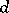 . It is therefore supposed, as a rule, that the function
. It is therefore supposed, as a rule, that the function  has the form
has the form  , where
, where 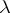 is some non-negative function of the error vector
is some non-negative function of the error vector 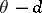 . If
. If 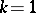 , it is often assumed that
, it is often assumed that 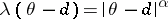 ,
, 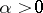 ; the most useful and mathematically the most convenient is the quadratic loss function
; the most useful and mathematically the most convenient is the quadratic loss function 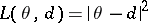 . For such a loss function the Bayesian estimator (Bayesian decision function)
. For such a loss function the Bayesian estimator (Bayesian decision function) 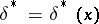 is defined as the function for which the minimum total loss
is defined as the function for which the minimum total loss
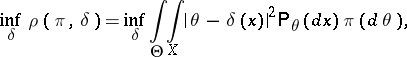 |
is attained, or, equivalently, for which the minimum conditional loss
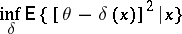 |
is attained. It follows that in the case of a quadratic loss function the Bayesian estimator 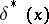 coincides with the a posteriori average
coincides with the a posteriori average 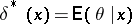 , and the Bayes risk is
, and the Bayes risk is
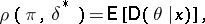 |
where 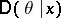 is the variance of the a posteriori distribution:
is the variance of the a posteriori distribution:
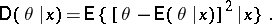 |
Example. Let 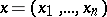 , where
, where  are independent identically-distributed random variables with normal distributions
are independent identically-distributed random variables with normal distributions 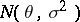 ,
, 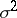 is known, while the unknown parameter
is known, while the unknown parameter 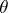 has the normal distribution
has the normal distribution 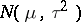 . Since the a posteriori distribution for
. Since the a posteriori distribution for 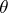 (where
(where  is given) is normal
is given) is normal 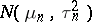 with
with
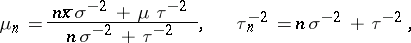 |
where 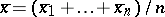 , it follows that for the quadratic loss function
, it follows that for the quadratic loss function 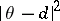 the Bayesian estimator is
the Bayesian estimator is 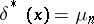 , while the Bayesian risk is
, while the Bayesian risk is 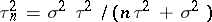 .
.
Comments
References
| [a1] | E. Sverdrup, "Laws and chance variations" , 1 , North-Holland (1967) pp. Chapt. 6, Section 4 |
Bayesian estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bayesian_estimator&oldid=19043