Graph colouring
An assignment of colours to the vertices and/or edges of a graph which displays certain properties. A regular vertex (edge) colouring is a colouring of the vertices (edges) of a graph in which any two adjacent vertices (edges) have different colours. A regular vertex colouring is often simply called a graph colouring. A graph is said to be  -colourable if there exists a regular vertex colouring of the graph by
-colourable if there exists a regular vertex colouring of the graph by 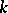 colours. The smallest number of colours which suffices for a regular vertex colouring of a graph
colours. The smallest number of colours which suffices for a regular vertex colouring of a graph 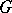 is called the chromatic number
is called the chromatic number  of
of 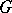 . If
. If  ,
, 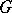 is said to be
is said to be 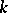 -chromatic. A graph is
-chromatic. A graph is  -chromatic if and only if it contains no simple cycles of odd length. If the maximum degree of the vertices of
-chromatic if and only if it contains no simple cycles of odd length. If the maximum degree of the vertices of 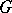 is
is  ,
, 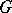 is always
is always  -colourable except in two cases: 1)
-colourable except in two cases: 1) 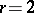 and
and 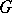 has a connected component which is a cycle of odd length; or 2)
has a connected component which is a cycle of odd length; or 2) 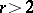 and the complete graph with
and the complete graph with 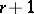 vertices is a connected component of
vertices is a connected component of 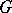 .
.
The following inequality is valid for the union of two graphs 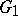 and
and 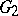 :
:
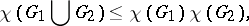 |
equality being attainable. Moreover, if 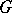 is such that
is such that 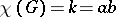 , then there exist subgraphs
, then there exist subgraphs  and
and 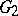 in
in 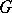 such that
such that 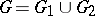 ,
, 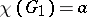 ,
, 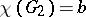 . If
. If 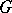 is a graph with
is a graph with  vertices and
vertices and 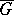 is the complementary graph to
is the complementary graph to 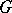 , then
, then
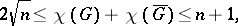 |
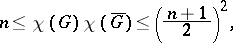 |
all the bounds being attainable. The chromatic number 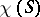 of a two-dimensional surface
of a two-dimensional surface 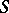 is the largest of the chromatic numbers of the graphs which can be regularly imbedded in
is the largest of the chromatic numbers of the graphs which can be regularly imbedded in 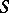 (cf. Graph imbedding). The equality
(cf. Graph imbedding). The equality
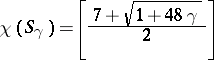 |
is valid for an orientable surface 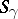 of genus
of genus 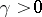 . If
. If 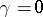 , this equation assumes the form
, this equation assumes the form 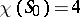 , which is the statement of the four-colour problem. Let
, which is the statement of the four-colour problem. Let 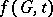 be the number of different regular colourings of a graph
be the number of different regular colourings of a graph 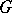 with numbered vertices with
with numbered vertices with 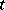 or fewer colours; then, for any graph
or fewer colours; then, for any graph 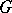 , the function
, the function 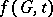 is a polynomial in the variable
is a polynomial in the variable 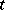 , called the chromatic polynomial of
, called the chromatic polynomial of 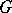 . Thus, the chromatic polynomial of any tree with
. Thus, the chromatic polynomial of any tree with  vertices has the form
vertices has the form 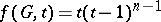 . The edge chromatic number (chromatic class)
. The edge chromatic number (chromatic class) 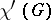 of
of 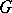 is the smallest number of colours sufficient for a regular colouring of the edges of
is the smallest number of colours sufficient for a regular colouring of the edges of 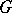 . If the maximum degree of the vertices of
. If the maximum degree of the vertices of 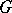 is
is 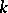 (multiple edges are permitted), then
(multiple edges are permitted), then
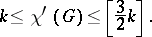 |
If, in addition, the multiplicity of each edge is at most  , then
, then 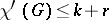 . In particular, for graphs without loops or multiple edges
. In particular, for graphs without loops or multiple edges  .
.
Problems involving graph colouring arise in design of communications, in radio-electronics, in planning of experiments, and in other fields.
References
| [1] | F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9 |
| [2] | O. Ore, "Theory of graphs" , Amer. Math. Soc. (1962) |
| [3] | C.E. Shannon, "A theorem on colouring the lines of a network" J. Math. Phys. , 28 (1949) pp. 148–151 |
Comments
Besides vertex colourings and edge colourings, the colourings of the domains (faces) of a planar map have also been studied. The four-colour problem mentioned in the article above (which is now the four-colour theorem) originally belonged to this category (see Graph, planar). Recent surveys on edge colourings are [a1] and [a2].
References
| [a1] | S. Fiorini, R.J. Wilson, "Edge-colourings of graphs" , Pitman (1977) |
| [a2] | S. Fiorini, R.J. Wilson, "Edge-colourings of graphs" L.W. Beineke (ed.) R.J. Wilson (ed.) , Selected Topics in Graph Theory , Acad. Press (1978) pp. Chapt. 5 |
| [a3] | R.J. Wilson, "Introduction to graph theory" , Longman (1985) |
| [a4] | R.C. Read, "An introduction to chromatic polynomials" J. Comb. Theory , 4 (1968) pp. 52–71 |
Graph colouring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Graph_colouring&oldid=19036