Riesz summation method

A method for summing series of numbers and functions; denoted by 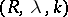. A series 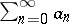is summable by the Riesz summation method 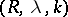to the sum if

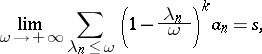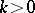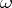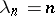where , , and is a continuous parameter. The method was introduced by M. Riesz [1] for the summation of Dirichlet series. The method is regular; when it is equivalent to the Cesàro summation method 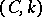(cf. Cesàro summation methods), and these methods are compatible (cf. Compatibility of summation methods).

Riesz considered also a method in which summability of the series 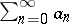is defined by means of the limit of the sequence 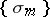, where

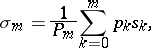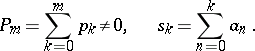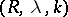This method is denoted by . The method is a modification of the method 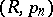(when 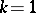) and is a generalization of it to the case of an arbitrary .

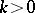References

[1]	M. Riesz, "Une méthode de sommation équivalente à la méthode des moyennes arithmétique" C.R. Acad. Sci. Paris , 152 (1911) pp. 1651–1654
[2]	F. Riesz, "Sur la sommation des séries de Dirichlet" C.R. Acad. Sci. Paris , 149 (1909) pp. 18–21
[3]	G.H. Hardy, M. Riesz, "The general theory of Dirichlet series" , Cambridge Univ. Press (1915)
[4]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)

References

[a1]	K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970)