World function
From Encyclopedia of Mathematics
The value of the integral
 |
taken along a geodesic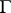 
joining two points 
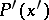and 
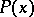in (geodesically-convex) space-time. Here 
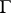is given by a parametrization 
, where 
is a canonical parameter and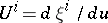 
. The world function is equal, up to sign, to half the square measure of the geodesic joining 
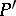and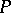 
, and is a two-point invariant in the sense that its value does not change under coordinate transformations in a neighbourhood of 
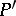and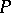 
.
In flat space-time there is a system of coordinates such that
 |
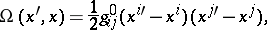where
 |
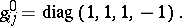References
| [1] | J.L. Synge, "Relativity: the general theory" , North-Holland & Interscience (1960) pp. Chapt. II |
How to Cite This Entry:
World function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=World_function&oldid=18986
World function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=World_function&oldid=18986
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article