Dirichlet density
Let 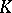 be an algebraic number field (cf. also Algebraic number) and let
be an algebraic number field (cf. also Algebraic number) and let 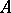 be a set of prime ideals (of the ring of integers
be a set of prime ideals (of the ring of integers 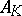 ) of
) of 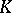 . If an equality of the form
. If an equality of the form
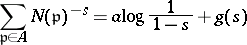 |
holds, where 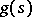 is regular in the closed half-plane
is regular in the closed half-plane 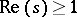 , then
, then 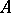 is a regular set of prime ideals and
is a regular set of prime ideals and  is called its Dirichlet density. Here,
is called its Dirichlet density. Here,  is the norm of
is the norm of 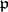 , i.e. the number of elements of the residue field
, i.e. the number of elements of the residue field 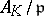 .
.
Examples.
i) The set of all prime ideals of  is regular with Dirichlet density
is regular with Dirichlet density 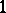 .
.
ii) Let 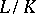 be a finite extension and
be a finite extension and 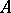 the set of all prime ideals
the set of all prime ideals 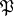 in
in 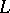 that are of degree
that are of degree 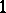 over
over 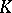 (i.e.
(i.e. 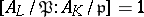 , where
, where 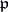 is the prime ideal
is the prime ideal 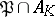 under
under 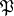 ). Then
). Then 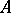 is regular with Dirichlet density
is regular with Dirichlet density 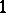 .
.
iii) Let 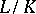 be a finite normal extension and
be a finite normal extension and 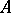 the set of all prime ideals
the set of all prime ideals  in
in 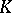 that split in
that split in 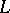 (i.e.
(i.e. 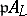 is a product of
is a product of 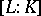 prime ideals in
prime ideals in 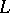 of degree
of degree 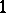 ). Then
). Then  is regular with Dirichlet density
is regular with Dirichlet density 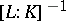 .
.
The notion of a Dirichlet density can be extended to not necessarily regular sets of prime ideals. Such a set 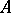 has Dirichlet density
has Dirichlet density  if
if
 |
References
| [a1] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990) pp. Sect. 7.2 (Edition: Second) |
Dirichlet density. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_density&oldid=18984