Element of best approximation

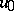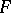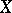An element in a given set that is a best approximation to a given element in a metric space , i.e. is such that

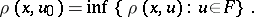This is a generalization of the classical concept of a polynomial of best approximation. The main questions concerning elements of best approximation are: their existence and uniqueness, their characteristic properties (see Chebyshev theorem), the properties of the operator that associates with each element 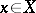the set of elements of best approximation (see Metric projection; Approximately-compact set), and numerical methods for the construction of elements of best approximation.