Constructive metric space
The concept of metric space used in constructive mathematics. The notion of recursive metric space has nearly the same meaning.
A list  , where
, where 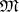 is some set of constructive objects (usually words over some alphabet) and
is some set of constructive objects (usually words over some alphabet) and 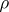 is an algorithm converting any pair of elements of
is an algorithm converting any pair of elements of 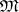 into a constructive real number (see Constructive analysis), is called a constructive metric space if for any
into a constructive real number (see Constructive analysis), is called a constructive metric space if for any 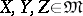 the following properties hold: 1)
the following properties hold: 1)  ; 2)
; 2) 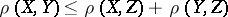 (here and in what follows the term "algorithm" is used in the sense of one of the precise notions of algorithm). The set
(here and in what follows the term "algorithm" is used in the sense of one of the precise notions of algorithm). The set 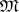 and the algorithm
and the algorithm  are respectively called the carrier and metric algorithm of the constructive metric space, and the elements of
are respectively called the carrier and metric algorithm of the constructive metric space, and the elements of 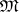 are the points of this constructive metric space. The axioms 1), 2) imply that
are the points of this constructive metric space. The axioms 1), 2) imply that 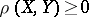 and
and 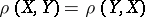 . Two points
. Two points  are called equivalent (respectively, distinct) in the constructive metric space
are called equivalent (respectively, distinct) in the constructive metric space 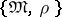 if
if 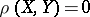 (respectively,
(respectively, 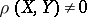 ).
).
Examples of constructive metric spaces. a) The space of natural numbers 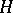 . The carrier of
. The carrier of 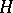 is the set of natural numbers (the natural numbers are treated as words of the form
is the set of natural numbers (the natural numbers are treated as words of the form 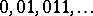 ), while the metric algorithm
), while the metric algorithm 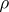 is given by
is given by 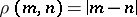 . The spaces
. The spaces 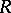 and
and 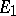 of rational and constructive real numbers, respectively, are defined similarly.
of rational and constructive real numbers, respectively, are defined similarly.
b) The  -dimension Euclidean space
-dimension Euclidean space 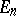 . The carrier of
. The carrier of 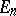 is the set of words of the form
is the set of words of the form 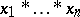 , where the
, where the 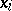 ,
, 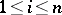 , are constructive real numbers, and the metric algorithm
, are constructive real numbers, and the metric algorithm 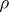 is constructed so that
is constructed so that
 |
c) The space 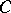 of uniformly-continuous constructive functions on the unit interval. The carrier of
of uniformly-continuous constructive functions on the unit interval. The carrier of 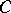 is the set of words of the form
is the set of words of the form 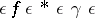 , where
, where  is a constructive function defined throughout the unit interval and
is a constructive function defined throughout the unit interval and 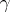 is an algorithm taking each natural number into a natural number so that
is an algorithm taking each natural number into a natural number so that
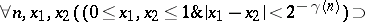 |
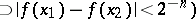 |
(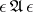 denotes the description (code) of the algorithm
denotes the description (code) of the algorithm 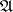 ). The metric algorithm
). The metric algorithm  is constructed so that
is constructed so that
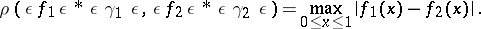 |
The complicated form of the carrier of the space 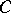 is necessary for the effective computability of the metric.
is necessary for the effective computability of the metric.
d) The Baire space of general recursive functions. The carrier of 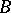 is the set of Gödel numbers of general recursive functions and the metric algorithm
is the set of Gödel numbers of general recursive functions and the metric algorithm 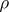 is constructed so that if
is constructed so that if  and
and 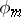 are general recursive functions with numbers
are general recursive functions with numbers  and
and  , then
, then 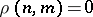 if
if 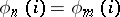 for any
for any 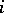 , and
, and 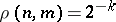 if
if 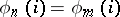 for
for 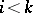 and
and 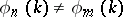 .
.
Let 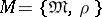 be a constructive metric space. An algorithm
be a constructive metric space. An algorithm 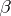 is called a sequence of points of
is called a sequence of points of 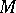 if
if 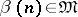 for every
for every  . The sequence
. The sequence 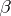 is called regular if
is called regular if 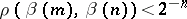 for
for  . A regular sequence
. A regular sequence 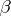 converges to the point
converges to the point 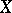 of the constructive metric space
of the constructive metric space 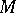 if
if 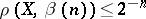 for any
for any  . A constructive metric space
. A constructive metric space  is called complete if there exists an algorithm that finds for each regular sequence
is called complete if there exists an algorithm that finds for each regular sequence 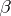 (of points of
(of points of  ) a point of
) a point of  to which
to which 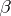 converges.
converges.  is called separable if there exists algorithms
is called separable if there exists algorithms 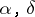 such that
such that 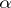 is a sequence of points of
is a sequence of points of 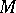 and for any
and for any 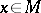 and any
and any  ,
,  is a natural number where
is a natural number where 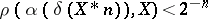 . All the spaces
. All the spaces 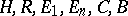 of the examples a)–d) are separable, the spaces
of the examples a)–d) are separable, the spaces 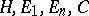 are complete as well. An example of a non-separable constructive metric space is given by considering a subspace of
are complete as well. An example of a non-separable constructive metric space is given by considering a subspace of 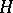 induced by a non-recursively enumerable set. Many of the results of the classical theory of metric spaces can be stated in terms of constructive metric spaces; in particular, the constructive variant of Hausdorff's theorem, stating that for any constructive metric space its completion can be constructed, is of great importance.
induced by a non-recursively enumerable set. Many of the results of the classical theory of metric spaces can be stated in terms of constructive metric spaces; in particular, the constructive variant of Hausdorff's theorem, stating that for any constructive metric space its completion can be constructed, is of great importance.
The process of completing a constructive metric space is a powerful means for introducing certain structures in constructive mathematics. Constructive real numbers are introduced in this way, and the natural analogues of the classical notions of measurable sets and functions, Lebesgue-integrable functions, etc., can be defined. One of the fundamental aims of the theory of constructive metric spaces is the study of algorithmic mappings that are well-defined with respect to some or other computable metrics.
Let  ,
, 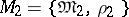 be two constructive metric spaces. By an algorithmic operator of type
be two constructive metric spaces. By an algorithmic operator of type  is meant an algorithm
is meant an algorithm 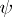 satisfying the following properties: a) if
satisfying the following properties: a) if 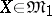 and
and 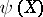 is defined, then
is defined, then 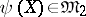 ; and b) if
; and b) if 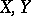 are equivalent points of
are equivalent points of 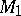 (that is,
(that is,  ) and if
) and if 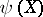 is defined, then
is defined, then  is defined and
is defined and 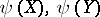 are equivalent points of
are equivalent points of 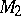 . Algorithmic operators of type
. Algorithmic operators of type 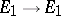 ,
, 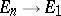 are constructive functions of one, respectively,
are constructive functions of one, respectively,  , variables; algorithmic operators of type
, variables; algorithmic operators of type 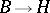 are conventionally called effective functionals (or effective operations).
are conventionally called effective functionals (or effective operations).
A fundamental result in the theory of algorithmic operators is Tseitin's theorem, which states that in the case of a complete separable constructive metric space 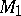 one can, for any algorithmic operator
one can, for any algorithmic operator 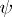 of type
of type 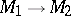 , construct for each
, construct for each  an algorithmically (recursively) enumerable set of balls covering the domain of definition of
an algorithmically (recursively) enumerable set of balls covering the domain of definition of 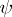 such that the oscillation of
such that the oscillation of 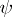 on any ball of this set does not exceed
on any ball of this set does not exceed 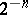 . This theorem implies the well-known result on the extendability of effective functionals to partial recursive functionals. Another important corollary of the above result is the theorem on the continuity of algorithmic operators: If
. This theorem implies the well-known result on the extendability of effective functionals to partial recursive functionals. Another important corollary of the above result is the theorem on the continuity of algorithmic operators: If 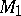 is a complete separable constructive metric space and
is a complete separable constructive metric space and 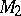 is an arbitrary constructive metric space, then for any algorithmic operator
is an arbitrary constructive metric space, then for any algorithmic operator 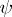 of type
of type  one can construct an algorithm
one can construct an algorithm 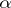 such that for any
such that for any  in the domain of definition of
in the domain of definition of 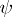 and any
and any  , the number
, the number 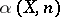 is a natural number, where
is a natural number, where 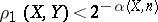 implies that
implies that 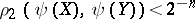 .
.
Using the same general methods as for the case of constructive metric spaces, one can develop a theory of constructive normed spaces and Hilbert spaces.
References
| [1] | G.S. Tseitin, "Algorithmic operators in constructive metric spaces" Trudy Mat. Inst. Steklov. , 67 (1962) pp. 295–361 (In Russian) |
| [2] | Y.N. Moschovakis, "Recursive metric spaces" Fund. Math. , 55 : 3 (1964) pp. 215–238 |
| [3] | N.A. Shanin, "Constructive real numbers and constructive function spaces" Trudy Mat. Inst. Steklov. , 67 (1962) pp. 15–294 (In Russian) |
| [4] | B.A. Kushner, "Lectures on constructive mathematical analysis" , Amer. Math. Soc. (1984) (Translated from Russian) |
Comments
The article above is only concerned with constructive analysis in the narrow sense of the Soviet school (see also Constructive mathematics). A different approach can be found in [a1], [a2]. For the notion of a recursive metric space see [a3].
References
| [a1] | E. Bishop, D.S. Bridges, "Constructive analysis" , Springer (1985) |
| [a2] | M.J. Beeson, "Foundations of constructive mathematics" , Springer (1985) |
| [a3] | O. Alberth, "Computable analysis" , McGraw-Hill (1980) |
Constructive metric space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Constructive_metric_space&oldid=18953