Cohomology of groups
Historically, the earliest theory of a cohomology of algebras.
With every pair 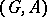 , where
, where 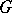 is a group and
is a group and 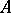 a left
a left 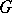 -module (that is, a module over the integral group ring
-module (that is, a module over the integral group ring 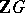 ), there is associated a sequence of Abelian groups
), there is associated a sequence of Abelian groups 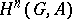 , called the cohomology groups of
, called the cohomology groups of 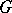 with coefficients in
with coefficients in 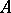 . The number
. The number  , which runs over the non-negative integers, is called the dimension of
, which runs over the non-negative integers, is called the dimension of 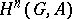 . The cohomology groups of groups are important invariants containing information both on the group
. The cohomology groups of groups are important invariants containing information both on the group 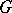 and on the module
and on the module 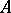 .
.
By definition,  is
is 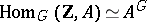 , where
, where 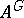 is the submodule of
is the submodule of 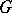 -invariant elements in
-invariant elements in 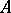 . The groups
. The groups 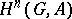 ,
, 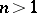 , are defined as the values of the
, are defined as the values of the  -th derived functor of the functor
-th derived functor of the functor 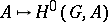 . Let
. Let
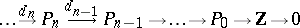 |
be some projective resolution of the trivial 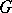 -module
-module 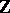 in the category of
in the category of  -modules, that is, an exact sequence in which every
-modules, that is, an exact sequence in which every 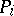 is a projective
is a projective 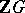 -module. Then
-module. Then 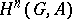 is the
is the  -th cohomology group of the complex
-th cohomology group of the complex
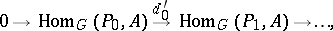 |
where 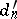 is induced by
is induced by 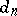 , that is,
, that is,  .
.
The homology groups of a group are defined using the dual construction, in which  is replaced everywhere by
is replaced everywhere by 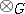 .
.
The set of functors 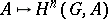 ,
, 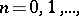 is a cohomological functor (see Homology functor; Cohomology functor) on the category of left
is a cohomological functor (see Homology functor; Cohomology functor) on the category of left 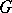 -modules.
-modules.
A module of the form 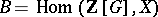 , where
, where 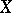 is an Abelian group and
is an Abelian group and  acts on
acts on 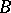 according to the formula
according to the formula
 |
is said to be co-induced. If 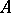 is injective or co-induced, then
is injective or co-induced, then 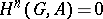 for
for 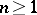 . Every module
. Every module 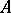 is isomorphic to a submodule of a co-induced module
is isomorphic to a submodule of a co-induced module 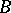 . The exact homology sequence for the sequence
. The exact homology sequence for the sequence
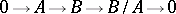 |
then defines isomorphisms 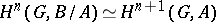 ,
, 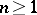 , and an exact sequence
, and an exact sequence
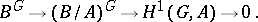 |
Therefore, the computation of the  -dimensional cohomology group of
-dimensional cohomology group of 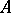 reduces to calculating the
reduces to calculating the  -dimensional cohomology group of
-dimensional cohomology group of 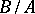 . This device is called dimension shifting.
. This device is called dimension shifting.
Dimension shifting enables one to give an axiomatic definition of cohomology groups, namely, they can be defined as a sequence of functors 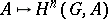 from the category of
from the category of  -modules into the category of Abelian groups forming a cohomological functor and satisfying the condition that
-modules into the category of Abelian groups forming a cohomological functor and satisfying the condition that  ,
, 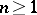 , for every co-induced module
, for every co-induced module  .
.
The groups 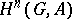 can also be defined as equivalence classes of exact sequences of
can also be defined as equivalence classes of exact sequences of 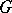 -modules of the form
-modules of the form
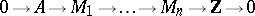 |
with respect to a suitably defined equivalence relation (see [1], Chapt. 3, 4).
To compute the cohomology groups, the standard resolution of the trivial 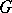 -module
-module  is generally used, in which
is generally used, in which 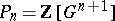 and, for
and, for 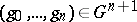 ,
,
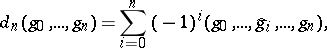 |
where the symbol  over
over 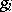 means that the term
means that the term 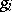 is omitted. The cochains in
is omitted. The cochains in 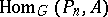 are the functions
are the functions 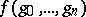 for which
for which 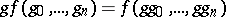 . Changing variables according to the rules
. Changing variables according to the rules 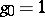 ,
,  ,
, 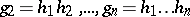 , one can go over to inhomogeneous cochains
, one can go over to inhomogeneous cochains 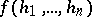 . The coboundary operation then acts as follows:
. The coboundary operation then acts as follows:
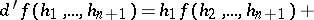 |
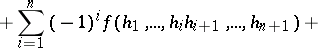 |
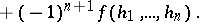 |
For example, a one-dimensional cocycle is a function 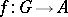 for which
for which 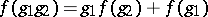 for all
for all 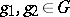 , and a coboundary is a function of the form
, and a coboundary is a function of the form 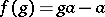 for some
for some 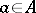 . A one-dimensional cocycle is also said to be a crossed homomorphism and a one-dimensional coboundary a trivial crossed homomorphism. When
. A one-dimensional cocycle is also said to be a crossed homomorphism and a one-dimensional coboundary a trivial crossed homomorphism. When 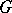 acts trivially on
acts trivially on 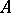 , crossed homomorphisms are just ordinary homomorphisms and all the trivial crossed homomorphisms are 0, that is,
, crossed homomorphisms are just ordinary homomorphisms and all the trivial crossed homomorphisms are 0, that is, 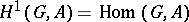 in this case.
in this case.
The elements of 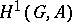 can be interpreted as the
can be interpreted as the 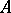 -conjugacy classes of sections
-conjugacy classes of sections 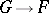 in the exact sequence
in the exact sequence  , where
, where 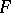 is the semi-direct product of
is the semi-direct product of 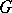 and
and 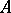 . The elements of
. The elements of 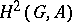 can be interpreted as classes of extensions of
can be interpreted as classes of extensions of 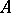 by
by 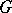 . Finally,
. Finally, 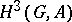 can be interpreted as obstructions to extensions of non-Abelian groups
can be interpreted as obstructions to extensions of non-Abelian groups 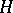 with centre
with centre 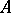 by
by 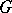 (see [1]). For
(see [1]). For 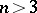 , there are no analogous interpretations known (1978) for the groups
, there are no analogous interpretations known (1978) for the groups 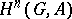 .
.
If 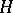 is a subgroup of
is a subgroup of  , then restriction of cocycles from
, then restriction of cocycles from 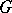 to
to 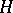 defines functorial restriction homomorphisms for all
defines functorial restriction homomorphisms for all  :
:
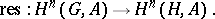 |
For 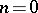 ,
,  is just the imbedding
is just the imbedding 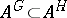 . If
. If 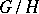 is some quotient group of
is some quotient group of 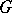 , then lifting cocycles from
, then lifting cocycles from 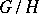 to
to 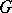 induces the functorial inflation homomorphism
induces the functorial inflation homomorphism
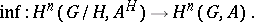 |
Let 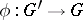 be a homomorphism. Then every
be a homomorphism. Then every 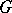 -module
-module 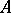 can be regarded as a
can be regarded as a 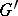 -module by setting
-module by setting 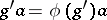 for
for 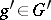 . Combining the mappings
. Combining the mappings 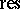 and
and 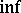 gives mappings
gives mappings 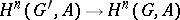 . In this sense
. In this sense 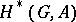 is a contravariant functor of
is a contravariant functor of 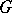 . If
. If  is a group of automorphisms of
is a group of automorphisms of 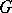 , then
, then 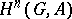 can be given the structure of a
can be given the structure of a 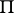 -module. For example, if
-module. For example, if  is a normal subgroup of
is a normal subgroup of 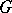 , the groups
, the groups  can be equipped with a natural
can be equipped with a natural 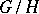 -module structure. This is possible thanks to the fact that inner automorphisms of
-module structure. This is possible thanks to the fact that inner automorphisms of 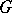 induce the identity mapping on the
induce the identity mapping on the 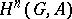 . In particular, for a normal subgroup
. In particular, for a normal subgroup 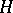 in
in 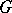 ,
, 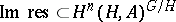 .
.
Let 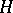 be a subgroup of finite index in the group
be a subgroup of finite index in the group 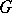 . Using the norm map
. Using the norm map 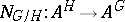 , one can use dimension shifting to define the functorial co-restriction mappings for all
, one can use dimension shifting to define the functorial co-restriction mappings for all  :
:
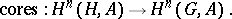 |
These satisfy 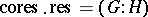 .
.
If 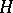 is a normal subgroup of
is a normal subgroup of  then there exists the Lyndon spectral sequence with second term
then there exists the Lyndon spectral sequence with second term  converging to the cohomology
converging to the cohomology 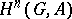 (see [1], Chapt. 11). In small dimensions it leads to the exact sequence
(see [1], Chapt. 11). In small dimensions it leads to the exact sequence
 |
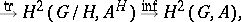 |
where 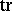 is the transgression mapping.
is the transgression mapping.
For a finite group 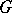 , the norm map
, the norm map 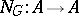 induces the mapping
induces the mapping 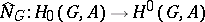 , where
, where 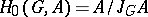 and
and 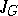 is the ideal of
is the ideal of 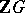 generated by the elements of the form
generated by the elements of the form  ,
, 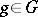 . The mapping
. The mapping 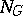 can be used to unite the exact cohomology and homology sequences. More exactly, one can define modified cohomology groups (also called Tate cohomology groups)
can be used to unite the exact cohomology and homology sequences. More exactly, one can define modified cohomology groups (also called Tate cohomology groups) 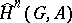 for all
for all  . Here
. Here
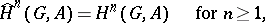 |
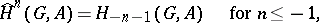 |
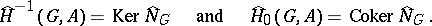 |
For these cohomology groups there exists an exact cohomology sequence that is infinite in both directions. A 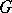 -module
-module 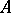 is said to be cohomologically trivial if
is said to be cohomologically trivial if 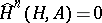 for all
for all  and all subgroups
and all subgroups 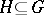 . A module
. A module 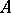 is cohomologically trivial if and only if there is an
is cohomologically trivial if and only if there is an 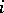 such that
such that 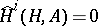 and
and 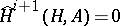 for every subgroup
for every subgroup  . Every module
. Every module 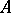 is a submodule or a quotient module of a cohomologically trivial module, and this allows one to use dimension shifting both to raise and to lower the dimension. In particular, dimension shifting enables one to define
is a submodule or a quotient module of a cohomologically trivial module, and this allows one to use dimension shifting both to raise and to lower the dimension. In particular, dimension shifting enables one to define  and
and 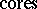 (but not
(but not 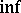 ) for all integral
) for all integral  . For a finitely-generated
. For a finitely-generated 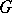 -module
-module 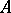 the groups
the groups 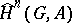 are finite.
are finite.
The groups 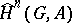 are annihilated on multiplication by the order of
are annihilated on multiplication by the order of  , and the mapping
, and the mapping 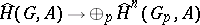 , induced by restrictions, is a monomorphism, where now
, induced by restrictions, is a monomorphism, where now  is a Sylow
is a Sylow 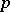 -subgroup (cf. Sylow subgroup) of
-subgroup (cf. Sylow subgroup) of 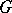 . A number of problems concerning the cohomology of finite groups can be reduced in this way to the consideration of the cohomology of
. A number of problems concerning the cohomology of finite groups can be reduced in this way to the consideration of the cohomology of 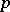 -groups. The cohomology of cyclic groups has period 2, that is,
-groups. The cohomology of cyclic groups has period 2, that is,  for all
for all  .
.
For arbitrary integers 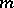 and
and  there is defined a mapping
there is defined a mapping
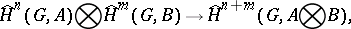 |
(called 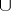 -product, cup-product), where the tensor product of
-product, cup-product), where the tensor product of 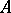 and
and 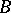 is viewed as a
is viewed as a 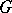 -module. In the special case where
-module. In the special case where 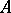 is a ring and the operations in
is a ring and the operations in 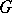 are automorphisms, the
are automorphisms, the 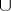 -product turns
-product turns 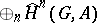 into a graded ring. The duality theorem for
into a graded ring. The duality theorem for  -products asserts that, for every divisible Abelian group
-products asserts that, for every divisible Abelian group 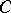 and every
and every 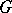 -module
-module 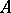 , the
, the 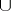 -product
-product
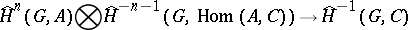 |
defines a group isomorphism between 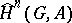 and
and 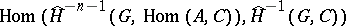 (see [2]). The
(see [2]). The 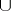 -product is also defined for infinite groups
-product is also defined for infinite groups 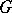 provided that
provided that 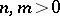 .
.
Many problems lead to the necessity of considering the cohomology of a topological group 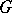 acting continuously on a topological module
acting continuously on a topological module  . In particular, if
. In particular, if  is a profinite group (the case nearest to that of finite groups) and
is a profinite group (the case nearest to that of finite groups) and 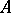 is a discrete Abelian group that is a continuous
is a discrete Abelian group that is a continuous 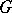 -module, one can consider the cohomology groups of
-module, one can consider the cohomology groups of  with coefficients in
with coefficients in 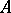 , computed in terms of continuous cochains [5]. These groups can also be defined as the limit
, computed in terms of continuous cochains [5]. These groups can also be defined as the limit 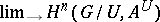 with respect to the inflation mapping, where
with respect to the inflation mapping, where 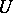 runs over all open normal subgroups of
runs over all open normal subgroups of 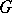 . This cohomology has all the usual properties of the cohomology of finite groups. If
. This cohomology has all the usual properties of the cohomology of finite groups. If 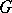 is a pro-
is a pro-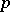 -group, the dimension over
-group, the dimension over 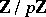 of the first and second cohomology groups with coefficients in
of the first and second cohomology groups with coefficients in 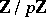 are interpreted as the minimum number of generators and relations (between these generators) of
are interpreted as the minimum number of generators and relations (between these generators) of  , respectively.
, respectively.
See [6] for different variants of continuous cohomology, and also for certain other types of cohomology groups. See Non-Abelian cohomology for cohomology with a non-Abelian coefficient group.
References
| [1] | S. MacLane, "Homology" , Springer (1963) |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) |
| [4] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [5] | H. Koch, "Galoissche Theorie der 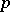 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [6] | Itogi Nauk. Mat. Algebra. 1964 (1966) pp. 202–235 |
Comments
The norm map 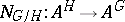 is defined as follows. Let
is defined as follows. Let 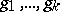 be a set of representatives of
be a set of representatives of 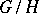 in
in 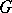 . Then
. Then 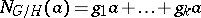 in
in 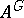 . For a definition of the transgression relation in general spectral sequences cf. Spectral sequence; for the particular case of group cohomology, where this gives a relation, sometimes called connection, between
. For a definition of the transgression relation in general spectral sequences cf. Spectral sequence; for the particular case of group cohomology, where this gives a relation, sometimes called connection, between 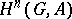 and
and 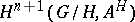 for all
for all 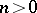 , cf. also [a1], Chapt. 11, Par. 9.
, cf. also [a1], Chapt. 11, Par. 9.
References
| [a1] | K.S. Brown, "Cohomology of groups" , Springer (1982) |
Cohomology of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohomology_of_groups&oldid=18938