Noetherian space
A topological space 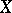 in which every strictly decreasing chain of closed subspaces breaks off. An equivalent condition is: Any non-empty family of closed subsets of
in which every strictly decreasing chain of closed subspaces breaks off. An equivalent condition is: Any non-empty family of closed subsets of 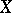 ordered by inclusion has a minimal element. Every subspace of a Noetherian space is itself Noetherian. If a space
ordered by inclusion has a minimal element. Every subspace of a Noetherian space is itself Noetherian. If a space 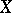 has a finite covering by Noetherian subspaces, then
has a finite covering by Noetherian subspaces, then 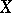 is itself Noetherian. A space
is itself Noetherian. A space 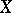 is Noetherian if and only if every open subset of
is Noetherian if and only if every open subset of 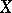 is quasi-compact. A Noetherian space
is quasi-compact. A Noetherian space 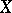 is the union of finitely many irreducible components.
is the union of finitely many irreducible components.
Examples of Noetherian spaces are some spectra of commutative rings (cf. Spectrum of a ring). For a ring 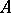 the space
the space 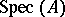 (the spectrum of
(the spectrum of  ) is Noetherian if and only if
) is Noetherian if and only if 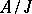 is a Noetherian ring, where
is a Noetherian ring, where 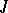 is the nil radical of
is the nil radical of 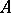 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Noetherian space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Noetherian_space&oldid=18927