Linear differential operator

in the narrow sense

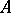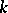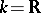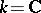An operator that acts on -valued functions ( or ) defined on an open set 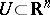, according to the formula

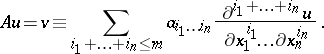(1)

Here 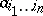are functions with values in the same field, called the coefficients of 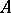. If the coefficients take values in the set of 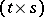-dimensional matrices over 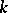, then the linear differential operator 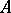is defined on vector-valued functions 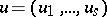and transforms them into vector-valued functions 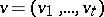. In the case 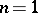it is called a linear ordinary differential operator, and in the case 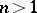it is called a linear partial differential operator.

Let 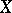be a differentiable manifold and let 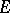and 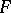be finite-dimensional vector bundles on 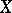(all of class 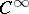, cf. Vector bundle). Let 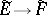be the sheaves (cf. Sheaf) of germs of sections of these bundles of the corresponding smoothness class. A linear differential operator in the wide sense 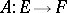is a sheaf mapping 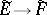satisfying the following condition: Every point 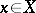has a coordinate neighbourhood 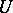within which the bundles are trivial, while the mapping

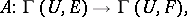where 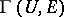is the space of sections of 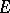over 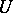, acts according to (1), in which local coordinates and the trivializations

are used. The smallest number 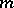such that (1) is suitable at all points 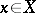is called the order of the linear differential operator 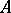. For example, every non-zero connection on 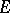is a linear differential operator 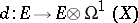of the first order. Another equivalent definition of a linear differential operator 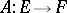is the following: It is a linear operator 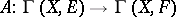satisfying the condition 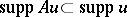, where 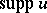is the support of .

A linear differential operator can be defined on wider function spaces. For example, if a positive metric is defined on 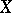and a scalar product is defined on the bundles 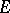and 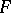, then the spaces of square-integrable sections of these bundles are defined. A linear differential operator defined by the local expressions (1) determines a linear unbounded operator 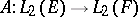. Under certain weak assumptions the latter may be closed as an operator on Hilbert spaces. This closure is also called a linear differential operator. In a similar way one can construct an operator that acts on Sobolev spaces or on spaces of more general scales.

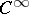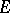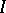A linear differential operator of class can be extended to an operator on spaces of generalized sections. Such an extension can be constructed by means of a formally adjoint operator. Let be the bundle dual to (that is, , where is the trivial one-dimensional bundle) and let be the bundle of differential forms on 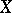of maximal degree. There is defined a bilinear mapping

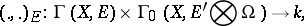which involves integration over 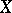. Here 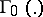is the space of sections with compact support. The formula

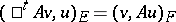uniquely defines a linear operator

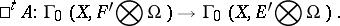It is induced by the linear differential operator 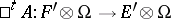which inside the coordinate neighbourhood 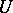has the expression

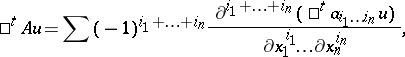if the bundle is trivialized by the choice of the section 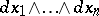. The linear differential operator 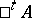is said to be formally adjoint with respect to .

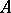In the space 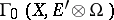convergence is defined according to the following rule: 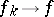if the union of the supports of the sections 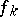belongs to a compact set and if in any coordinate neighbourhood 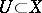over which there is a trivialization of 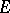, the vector-valued functions converge uniformly to 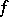together with all partial derivatives with respect to local coordinates. The space of all linear functionals is called the space of generalized sections of 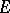and is denoted by 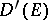. The operator 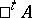takes convergent sequences to convergent sequences and therefore generates an adjoint operator 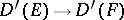. The latter coincides with 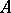on the subspace 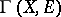and is called the extension of the given linear differential operator to the space of generalized sections. One also considers other extensions of linear differential operators, to spaces of generalized sections of infinite order, to the space of hyperfunctions, etc.

A linear differential operator of infinite order is understood to be an operator that acts in some space of analytic functions (sections) and is defined by (1), in which the summation is over an infinite set of indices .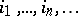

The following property characterizes linear differential operators. A sequence 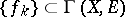is said to converge to a section 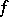if 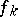tends uniformly to 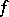together with all partial derivatives in any coordinate neighbourhood that has compact closure. A linear operator 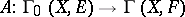that takes convergent sequences to convergent sequences is a linear differential operator of order at most 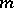if and only if for any 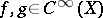the function

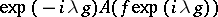(2)

is a polynomial in the parameter 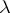of degree at most 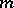. If this condition is replaced by the assumption that (2) is represented by an asymptotic power series, then one obtains a definition of a linear pseudo-differential operator.

Suppose that the manifold 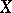and also the bundles 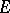and 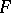are endowed with a 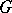-structure, where is a group. Then the action of this group on any linear differential operator 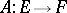is defined by the formula

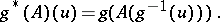A linear differential operator 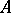is said to be invariant with respect to 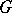if 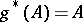for all .

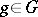A bundle of jets is an object dual to the space of a linear differential operator. Again suppose that 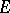is a vector bundle on a manifold 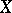of class 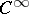. A bundle of 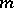-jets of sections of 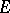is a vector bundle 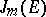on 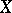whose fibre over a point is equal to 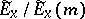, where 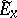is a fibre of the bundle 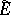of germs of sections of 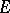and 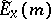is the subspace of this fibre consisting of germs of sections for which all derivatives up to order 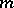inclusive vanish at . The linear differential operator 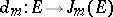that acts according to the rule: the value of the section 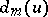at is equal to the image of the section in the quotient space 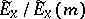, is said to be universal. Next, suppose that 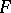is a bundle on 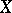and that 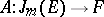is a bundle homomorphism, that is, a linear differential operator of order zero. The composite

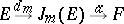(3)

is a linear differential operator of order at most 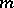. Conversely, every linear differential operator of order at most 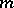can be represented uniquely as a composition (3).

The symbol (principal system) of a linear differential operator 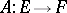is the family of linear mappings

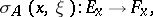depending on a point 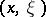of the cotangent bundle 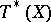. They act according to the formula 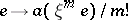, where is the homomorphism involved in (3), 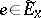, and 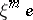is the element of 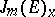equal to the image of 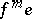, where 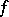is the germ of a function of class 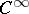such that 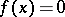, 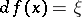. If 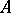has the form (1), then

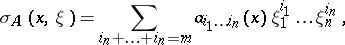where 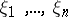are the coordinates in a fibre of the bundle ; thus, the symbol is a form of degree 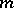, homogeneous in . In accordance with this construction of the symbol one introduces the concept of a characteristic. A characteristic of a linear differential operator 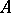is a point 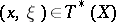at which the symbol 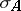has non-zero kernel.

The classification adopted in the theory of linear differential operators refers mainly to linear differential operators that act in bundles of the same dimension, in fact to operators of the form (1) where the coefficients are square matrices. A linear differential operator is said to be elliptic if it does not have real characteristics 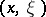with 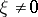(cf. also Elliptic partial differential equation). This class is characterized by the best local properties of solutions of the equation 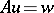, and also by the fact that boundary value problems in bounded domains are well-posed. The class of hyperbolic linear differential operators is also distinguished by a condition imposed only on the characteristics (cf. Hyperbolic partial differential equation). The property of being hyperbolic is closely connected with the well-posedness of the Cauchy problem with non-analytic data. The class of linear differential operators of principal type is specified by a condition imposed only on the symbol (cf. Principal type, partial differential operator of). A theory of local solvability and smoothness of solutions has been developed for such operators. The class of parabolic linear differential operators is distinguished by a condition related not only to the symbol but also to some lower-order terms (cf. Parabolic partial differential equation). Typical for parabolic linear differential operators are the mixed problem and the Cauchy problem with conditions at infinity. The class of hypo-elliptic linear differential operators is specified by the following informal condition: Every a priori generalized solution of the equation 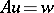with right-hand side from 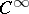itself belongs to 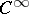. A number of formal conditions on the expression (1) that guarantee that the operator is hypo-elliptic are known.

Apart from these fundamental types of linear differential operators, one sometimes talks about linear differential operators of mixed or variable type (cf. also Mixed-type differential equation), of linear differential operators of composite type, etc. One also considers problems in unbounded domains with conditions at infinity, boundary value problems with a free boundary, problems of spectral theory, problems of optimal control, etc.

A complex of linear differential operators is a sequence of linear differential operators

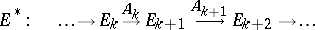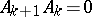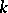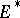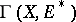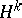in which for all . The cohomology of a complex of linear differential operators is the cohomology of the complex of vector spaces . Let be the cohomology of this complex at the 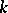-th term. The sum 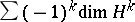is called the index of the complex of linear differential operators. Thus, the index of an elliptic complex of linear differential operators (that is, such that only finitely many 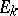are non-zero, and the complex formed by the symbols of the linear differential operators 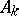is exact at all points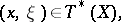 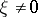) is finite in the case of compact 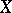, and the search for formulas that express the index of such a complex in terms of its symbol is the content of a number of investigations that combine the theory of linear differential operators with algebraic geometry and algebraic topology (see Index formulas).

The definition of a symbol (and of characteristics) described above is not entirely satisfactory for linear differential operators that act in bundles of dimension greater than 1. One of the reasons for this is the fact that the equality 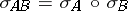may be violated. The following complicated construction, which replaces the concept of the symbol, is more adequate. For every bundle 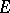on a manifold 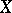of class 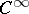one considers the sheaf 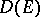of germs of linear differential operators 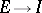, where 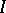is the one-dimensional trivial bundle. By definition, the value of this sheaf on an open set 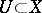is the totality of all linear differential operators 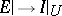. 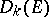Let be the subsheaf of it formed by the operators of order at most 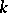. 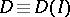On there is a structure of a sheaf of (non-commutative) algebras, and 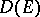has a structure of a left module over 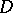, where the action of 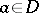on 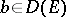is equal to the composite 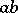. A given linear differential operator 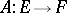determines a morphism of left 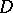-modules 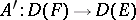according to the law of composition 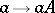. 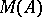Let be the cokernel of this morphism. There is an exact sequence of left 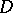-modules

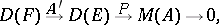(4)

and the 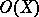-submodules 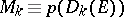, 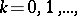form an increasing filtration in 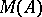. The graded 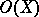-module

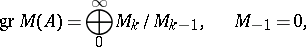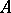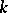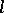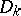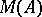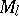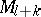is called the symbol module of the linear differential operator . Since for any and the action of on takes into , in 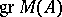there is a structure of a graded module over the graded algebra 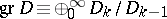. The annihilator of this module is a homogeneous ideal in 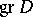. The characteristic manifold of the operator 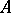is the set of zeros of this ideal. Since the algebra 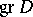is isomorphic to the symmetric algebra of the tangent bundle 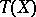, the characteristic manifold is canonically imbedded in 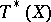, and its intersection with every fibre is an algebraic cone.

If the manifold 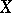and the given bundles have real or complex analytic structure, then the characteristic manifold coincides with the set of roots of the ideal 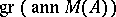. In this case it is a closed analytic subset of 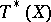, and if it is not empty its dimension is at least 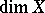. In the case when this dimension is equal to 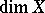, the linear differential operator 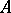is said to be maximally overdetermined, or holonomic.

The formal theory of general linear differential operators is concerned with the concepts of formal integrability and the resolvent. The property of formal integrability, formalized in the dual terminology of jets, is equivalent to the condition that the -module 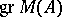is locally free. The resolvent of a linear differential operator 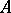is understood to be the sequence, extending (4),

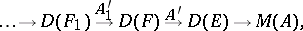in which all the 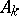, 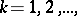are linear differential operators. In particular, 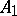is called the compatibility operator for 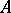. Formal integrability ensures the local existence of the resolvent.

In the literature use is made of the terms "overdetermined" and "underdetermined" for systems of differential equations; however, there is no satisfactory general definition. The following could serve as an approximation to such a definition: There is a non-zero linear differential operator 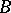such that 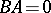(overdetermination), 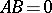(underdetermination). For example, the linear differential operator 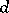equal to the restriction of the operator of exterior differentiation to forms of degree 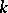on a manifold 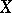of dimension is underdetermined for 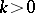, overdetermined for 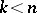and holonomic for .

The main problems studied for general linear differential operators are the following: The solvability of an equation with right-hand side 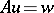if a compatibility condition 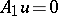is satisfied; the possibility of extending solutions of the equation 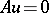to a larger domain (an effect connected with overdetermination); and the representation of the general solution in terms of a solution of special form. The last problem can be stated more specifically for invariant operators, for example for linear differential operators in with constant or periodic coefficients: To describe a representation of a group 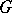in the space of solutions as an integral (in some sense) over all indecomposable subrepresentations. In determining operators with constant coefficients such a representation is specified by an integral with respect to exponents (exponential representation), and for operators with periodic coefficients by an integral with respect to Floquet-generalized solutions.

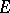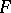Linear differential operators are also defined on arbitrary algebraic structures. Let be a commutative ring and let and be 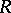-modules. A mapping of sets 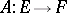is called a linear differential operator of order at most 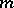if it is additive and for any element 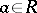the mapping 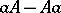is a linear differential operator of order at most 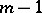. A linear differential operator of order at most 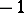means the zero mapping. In particular, a linear differential operator of order zero is a homomorphism of 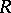-modules, and conversely. Every derivation (cf. Derivation in a ring) 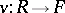is a linear differential operator of the first order (or equal to zero). If 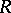is an algebra over a field 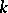, then a linear differential operator over 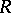is a linear differential operator over the ring 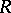that is a 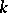-linear mapping. Such a linear differential operator has a number of the formal properties of ordinary linear differential operators. If 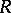is the algebra of all formal power series over 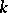or the algebra of convergent power series over 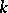, and if 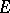and 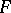are free 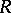-modules of finite type, then every linear differential operator 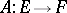of order at most 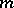can be written uniquely in the form (1).

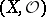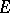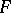Let be a ringed space and let and be 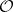-modules. A linear differential operator 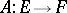is any sheaf morphism that acts in the fibres over every point 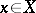like a linear differential operator over the ring (algebra) 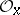. Linear differential operators that act in modules or sheaves of modules have been used in a number of questions in algebraic geometry.

References

[1]	J. Peetre, "Uniqueness in the Cauchy problem for elliptic equations with double characteristics" Math. Scand. , 8 (1960) pp. 116–120
[2]	L. Hörmander, , Pseudo-differential operators , Moscow (1967) pp. 63–87; 166–296; 297–367 (In Russian; translated from English)
[3]	I.N. Bernshtein, "The analytic continuation of generalized functions with respect to a parameter" Funct. Anal. Appl. , 6 : 4 (1972) pp. 273–285 Funktsional. Anal. i Prilozhen. , 6 : 4 (1972) pp. 26–40
[4]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[5]	A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)
[6]	L.V. Hörmander, "The analysis of linear partial differential operators" , 1–4 , Springer (1983–1985)
[7]	V.P. Palamodov, "Linear differential operators with constant coefficients" , Springer (1970) (Translated from Russian)
[8]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[9]	R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965)
[10]	V.P. Palamodov, "Systems of linear differential equations" Itogi Nauk. Mat. Anal. 1968 (1969) pp. 5–37 (In Russian)
[11]	J.-E. Björk, "Rings of differential operators" , North-Holland (1979)
[12]	M. Kashiwara, "Microfunctions and pseudodifferential equations" H. Komatsu (ed.) , Hyperfunctions and pseudodifferential equations. Proc. Conf. Katata, 1971 , Lect. notes in math. , 287 , Springer (1973) pp. 265–529

Comments

Cf. also Differential operator; Differential operator on a module; 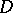-module; Hyperfunction; Microlocal analysis.