Quasi-normal space

A regular space in which two disjoint -sets have disjoint neighbourhoods. Every -space in which any two disjoint -sets have disjoint neighbourhoods is a quasi-normal space. Only for the quasi-normal spaces does the Stone–Čech compactification coincide with the space . The following theorem provides a large supply of non-normal quasi-normal spaces: The product of any number of separated metric spaces is quasi-normal.

References

[1]	V.I. Zaitsev, "Projection spectra" Trans. Moscow Math. Soc. , 27 (1972) pp. 135–199 Trudy Moskov. Mat. Obshch. , 27 (1972) pp. 129–193
[2]	E.V. Shchepin, "On the bicompact Ponomarev–Zaicev extension and the so-called spectral parasite" Math. USSR Sb. , 17 (1972) pp. 317–326 Mat. Sb. , 88 : 2 (1972) pp. 316–325

Comments

Quasi-normal spaces arose in the study of the spectrum of a topological space (cf. also Spectrum of spaces). This spectrum is obtained as follows. A partition of a space is a finite collection of canonical closed sets (cf. Canonical set) that covers and the elements of which have disjoint interiors. The set of all these partitions is partially ordered by: if and only if 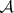refines . The nerve 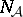of 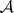(cf. Nerve of a family of sets) is the complex of subfamilies of 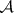that have a non-empty intersection. There is an obvious simplicial mapping 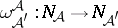if 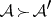. 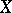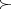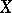If the set of partitions of is (upward) directed by , then the inverse spectrum is the spectrum of and is denoted by 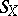. To obtain a suitable limit of this spectrum one takes the set 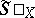of maximal threads of . 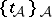A thread is a choice of simplexes with 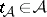for all and such that 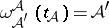whenever 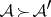. A thread is maximal if whenever 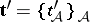is another thread such that 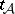is a face of 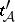for every 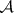, one has 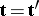. The basic open sets are the sets of the form .

The space , first introduced in [a3], is the space of all maximal centred systems of canonical closed sets topologized in the usual way, i.e. by taking the collection as a base for the closed sets of 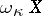, where 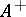is the set of maximal centred systems to which 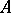belongs.

It turns out that there is a natural homeomorphism from 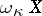onto 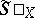. Thus, for quasi-normal spaces one has .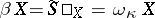

A 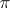-set is a finite intersection of closures of open sets. A -space, first introduced in [1], is a semi-regular (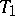-) space all open sets of which are unions of 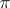-sets. I.e., a 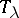-space is a semi-regular (-) space (the canonical open sets form a base for the topology) in which the canonical closed sets form a net (of sets in a topological space), i.e. if 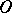is open and 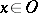, then there is a canonical closed set such that .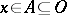

References

[a1]	A. Kurosh, "Kombinatorischer Aufbau der bikompakten topologischen Räume" Compositio Math. , 2 (1935) pp. 471–476
[a2]	V.I. Zaitsev, "Finite spectra of topological spaces and their limit spaces" Math. Ann. , 179 (1968–1969) pp. 153–174
[a3]	V.I. Ponomarev, "Paracompacta: their projection spectra and continuous mappings" Mat. Sb. , 60 (102) (1963) pp. 89–119 (In Russian)