Pure submodule
in the sense of Cohn
A submodule 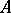 of a right
of a right  -module
-module 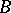 such that for any left
such that for any left 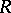 -module
-module 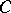 the natural homomorphism of Abelian groups
the natural homomorphism of Abelian groups
 |
is injective. This is equivalent to the following condition: If the system of equations
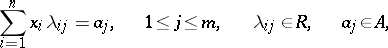 |
has a solution in 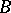 , then it has a solution in
, then it has a solution in  (cf. Flat module). Any direct summand is a pure submodule. All submodules of a right
(cf. Flat module). Any direct summand is a pure submodule. All submodules of a right 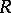 -module are pure if and only if
-module are pure if and only if 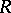 is a regular ring (in the sense of von Neumann).
is a regular ring (in the sense of von Neumann).
In the case of Abelian groups (that is, 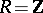 ), the following assertions are equivalent: 1)
), the following assertions are equivalent: 1) 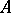 is a pure (or serving) subgroup of
is a pure (or serving) subgroup of 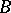 (cf. Pure subgroup); 2)
(cf. Pure subgroup); 2) 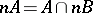 for every natural number
for every natural number  ; 3)
; 3) 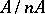 is a direct summand of
is a direct summand of 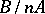 for every natural number
for every natural number  ; 4) if
; 4) if 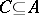 and
and 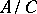 is a finitely-generated group, then
is a finitely-generated group, then 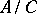 is a direct summand of
is a direct summand of 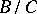 ; 5) every residue class in the quotient group
; 5) every residue class in the quotient group  contains an element of the same order as the residue class; and 6) if
contains an element of the same order as the residue class; and 6) if 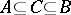 and
and 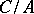 is finitely generated, then
is finitely generated, then 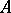 is a direct summand of
is a direct summand of 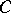 . If property 2) is required to hold only for prime numbers
. If property 2) is required to hold only for prime numbers  , then
, then 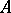 is called a weakly-pure subgroup.
is called a weakly-pure subgroup.
The axiomatic approach to the notion of purity is based on the consideration of a class of monomorphism 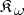 subject to the following conditions (here
subject to the following conditions (here 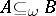 means that
means that 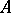 is a submodule of
is a submodule of 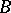 and that the natural imbedding belongs to
and that the natural imbedding belongs to 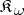 ): P0') if
): P0') if 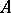 is a direct summand of
is a direct summand of 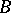 , then
, then 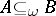 ; P1') if
; P1') if 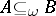 and
and 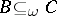 , then
, then 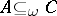 ; P2') if
; P2') if 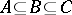 and
and 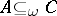 , then
, then 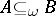 ; P3') if
; P3') if 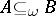 and
and 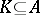 , then
, then 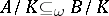 ; and P4') if
; and P4') if 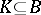 ,
, 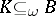 and
and 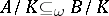 , then
, then 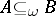 . Taking the class
. Taking the class 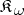 instead of the class of all monomorphisms leads to relative homological algebra. For example, a module
instead of the class of all monomorphisms leads to relative homological algebra. For example, a module 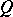 is called
is called 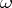 -injective if
-injective if 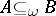 implies that any homomorphism from
implies that any homomorphism from 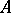 into
into 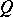 can be extended to a homomorphism from
can be extended to a homomorphism from 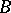 into
into 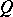 (cf. Injective module). A pure injective Abelian group is called algebraically compact. The following conditions on an Abelian group
(cf. Injective module). A pure injective Abelian group is called algebraically compact. The following conditions on an Abelian group 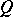 are equivalent:
are equivalent: 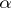 )
) 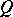 is algebraically compact;
is algebraically compact; 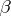 )
) 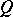 splits as a direct summand of any group that contains it as a pure subgroup;
splits as a direct summand of any group that contains it as a pure subgroup; 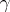 )
) 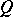 is a direct summand of a group that admits a compact topology; and
is a direct summand of a group that admits a compact topology; and 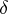 ) a system of equations over
) a system of equations over 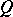 is solvable if every finite subsystem of it is solvable.
is solvable if every finite subsystem of it is solvable.
References
| [1] | A.P. Mishina, L.A. Skornyakov, "Abelian groups and modules" , Amer. Math. Soc. (1976) (Translated from Russian) |
| [2] | E.G. Sklyarenko, "Relative homological algebra in categories of modules" Russian Math. Surveys , 33 : 3 (1978) pp. 97–137 Uspekhi Mat. Nauk , 33 : 3 (1978) pp. 85–120 |
| [3] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
| [4] | L. Fuchs, "Infinite abelian groups" , 1–2 , Acad. Press (1970–1973) |
Comments
References
| [a1] | J. Rotman, "Introduction to homological algebra" , Acad. Press (1979) |
Pure submodule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pure_submodule&oldid=18846