Quasi-invariant measure
A measure on a space that is equivalent to itself under "translations" of this space. More precisely: Let 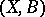 be a measurable space (that is, a set
be a measurable space (that is, a set 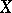 with a distinguished
with a distinguished 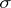 -algebra
-algebra 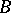 of subsets of it) and let
of subsets of it) and let 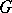 be a group of automorphisms of it (that is, one-to-one transformations
be a group of automorphisms of it (that is, one-to-one transformations 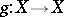 that are measurable together with their inverses
that are measurable together with their inverses 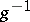 with respect to the
with respect to the 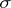 -algebra
-algebra 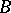 ). A measure
). A measure 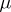 on
on 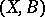 is said to be quasi-invariant (with respect to
is said to be quasi-invariant (with respect to 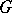 ) if for any
) if for any 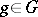 the transformed measure
the transformed measure 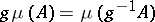 ,
, 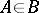 , is equivalent to the measure
, is equivalent to the measure 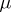 (that is, these measures are absolutely continuous with respect to each other, cf. Absolute continuity). If
(that is, these measures are absolutely continuous with respect to each other, cf. Absolute continuity). If 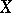 is a topological homogeneous space with a continuous locally compact group of automorphisms
is a topological homogeneous space with a continuous locally compact group of automorphisms 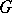 (that is,
(that is, 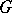 acts transitively on
acts transitively on 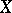 and is endowed with a topology such that the mapping
and is endowed with a topology such that the mapping 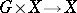 ,
, 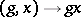 , is continuous with respect to the product topology on
, is continuous with respect to the product topology on 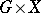 ) and
) and 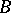 is the Borel
is the Borel 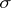 -algebra with respect to the topology on
-algebra with respect to the topology on 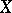 , then there exists a quasi-invariant measure that is unique up to equivalence [1]. In particular, a measure on
, then there exists a quasi-invariant measure that is unique up to equivalence [1]. In particular, a measure on 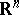 is quasi-invariant with respect to all shifts
is quasi-invariant with respect to all shifts 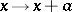 ,
, 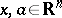 , if and only if it is equivalent to Lebesgue measure. If the group of transformations is not locally compact, there need not be a quasi-invariant measure; this is the case, for example, in a wide class of infinite-dimensional topological vector spaces [2].
, if and only if it is equivalent to Lebesgue measure. If the group of transformations is not locally compact, there need not be a quasi-invariant measure; this is the case, for example, in a wide class of infinite-dimensional topological vector spaces [2].
References
| [1] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
Comments
Thus, a quasi-invariant measure is a generalization of a Haar measure on a topological group. On a locally compact group with left Haar measure 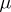 a measure is left quasi-invariant (quasi-invariant under left translations) if and only if it is equivalent to
a measure is left quasi-invariant (quasi-invariant under left translations) if and only if it is equivalent to 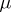 .
.
There exists no quasi-invariant measure on an infinite-dimensional Hilbert space with respect to the group of all translations (and so, in particular, no Haar measure). Let 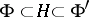 be a rigged Hilbert space, with
be a rigged Hilbert space, with 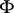 a nuclear space with inner product
a nuclear space with inner product  ,
, 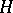 the completion of
the completion of 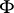 , and
, and 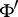 the dual of
the dual of 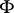 . Each
. Each 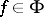 defines an element
defines an element 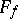 in
in 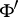 , the functional
, the functional 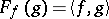 . A measure
. A measure 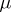 on
on 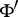 is quasi-invariant if
is quasi-invariant if 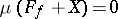 for all
for all 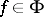 and
and 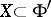 with
with 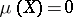 , i.e. if it is quasi-invariant with respect to the group of translations
, i.e. if it is quasi-invariant with respect to the group of translations 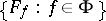 . There exist quasi-invariant measures on such dual spaces of nuclear spaces, [2], Chapt. IV, §5.2.
. There exist quasi-invariant measures on such dual spaces of nuclear spaces, [2], Chapt. IV, §5.2.
Quasi-invariant measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-invariant_measure&oldid=18836