Coherent analytic sheaf
A coherent sheaf of 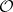 modules on an analytic space
modules on an analytic space 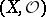 . A space
. A space 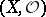 is said to be coherent if
is said to be coherent if 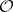 is a coherent sheaf of rings. Any analytic space over an algebraically closed field is coherent. The most important examples of a coherent analytic sheaf on such a space
is a coherent sheaf of rings. Any analytic space over an algebraically closed field is coherent. The most important examples of a coherent analytic sheaf on such a space 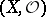 are a locally free sheaf (that is, an analytic sheaf locally isomorphic to the sheaf
are a locally free sheaf (that is, an analytic sheaf locally isomorphic to the sheaf  ) and also the sheaf of ideals of an analytic set
) and also the sheaf of ideals of an analytic set 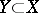 , that is, the sheaf of germs of analytic functions equal to
, that is, the sheaf of germs of analytic functions equal to  on
on 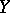 , [1].
, [1].
If 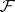 is a coherent analytic sheaf on a complex-analytic space
is a coherent analytic sheaf on a complex-analytic space  , then the space of its sections,
, then the space of its sections, 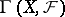 , is endowed with a natural topology turning it into a Fréchet space when
, is endowed with a natural topology turning it into a Fréchet space when 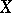 is separable. For
is separable. For 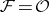 , this topology is the same as the topology of uniform convergence of analytic functions on compacta. In this case,
, this topology is the same as the topology of uniform convergence of analytic functions on compacta. In this case, 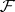 becomes a Fréchet sheaf, that is, for arbitrary open sets
becomes a Fréchet sheaf, that is, for arbitrary open sets 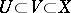 the restriction mapping
the restriction mapping 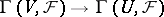 is continuous. An analytic homomorphism of coherent sheaves
is continuous. An analytic homomorphism of coherent sheaves  induces a continuous linear mapping
induces a continuous linear mapping 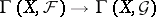 . If
. If 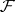 is a coherent analytic sheaf on
is a coherent analytic sheaf on 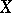 and
and 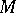 is a submodule of
is a submodule of 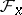 ,
,  , then the submodule
, then the submodule  is closed in
is closed in 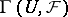 for any neighbourhood
for any neighbourhood 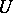 of
of  . The cohomology spaces
. The cohomology spaces 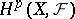 also have a natural topology, which is not, in general, separable for
also have a natural topology, which is not, in general, separable for  (they are quotient spaces of Fréchet spaces) [2], [4].
(they are quotient spaces of Fréchet spaces) [2], [4].
Coherent analytic sheaves were introduced in connection with problems in the theory of analytic functions on domains in 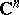 (see [3], [5]). Later they and their cohomology became a fundamental tool in the global theory of analytic spaces. Criteria for the vanishing of cohomology with values in a coherent analytic sheaf (cf. Kodaira theorem; Ample vector bundle; Stein space) as well as criteria for its finiteness and separability (see Finiteness theorems in the theory of analytic spaces) play an important role in this theory.
(see [3], [5]). Later they and their cohomology became a fundamental tool in the global theory of analytic spaces. Criteria for the vanishing of cohomology with values in a coherent analytic sheaf (cf. Kodaira theorem; Ample vector bundle; Stein space) as well as criteria for its finiteness and separability (see Finiteness theorems in the theory of analytic spaces) play an important role in this theory.
See also Vector bundle, analytic; Duality in the theory of analytic spaces.
References
| [1] | S.S. Abhyankar, "Local analytic geometry" , Acad. Press (1964) |
| [2] | C. Banica, O. Stanasila, "Algebraic methods in the global theory of complex spaces" , Wiley (1976) (Translated from Rumanian) |
| [3] | H. Cartan, "Idéaux et modules de fonctions analytiques de variables complexes" Bull. Soc. Math. France , 78 (1950) pp. 28–64 |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [5] | K. Oka, "Sur les fonctions analytiques de plusieurs variables (VII. Sur quelques notions arithmétiques)" Bull. Soc. Math. France , 78 (1950) pp. 1–27 |
Comments
See also Coherent sheaf.
References
| [a1] | H. Grauert, R. Remmert, "Coherent analytic sheaves" , Springer (1984) (Translated from German) |
Coherent analytic sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coherent_analytic_sheaf&oldid=18834