Projective group
in 
variables over a skew-field 
The group 
of transformations of the 
-dimensional projective space 
induced by the linear transformations of 
. There is a natural epimorphism
 |
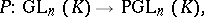with as kernel the group of homotheties (cf. Homothety) of 
, which is isomorphic to the multiplicative group 
of the centre 
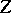of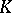 
. The elements of 
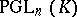, called projective transformations, are the collineations (cf. Collineation) of 
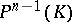. Along with 
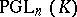, which is also called the full projective group, one also considers the unimodular projective group 
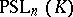, and, in general, groups of the form 
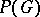, where 
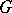is a linear group.
For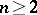 
the group 
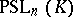is simple, except for the two cases 
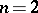and 
or 3. If 
is the finite field of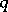 
elements, then
 |
 |
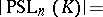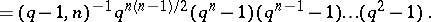References
| [1] | J.A. Dieudonné, "La géométrie des groupes classiques" , Springer (1955) |
Comments
The groups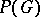 
for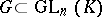 
are the images of 
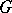under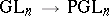 
. For a brief resumé on the orders of the other finite classical groups, like 
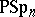, and their simplicity cf. e.g. [a1].
References
| [a1] | R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972) pp. Chapt. 1 |
Projective group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_group&oldid=18829