Stochastic differential equation

for a process with respect to a Wiener process

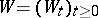
An equation of the form

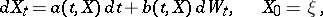(1)

where 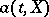and are non-anticipative functionals, and the random variable 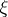plays the part of the initial value. There are two separate concepts for a solution of a stochastic differential equation — strong and weak.

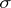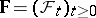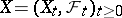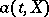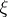Let be a probability space with an increasing family of -algebras , and let be a Wiener process. One says that a continuous stochastic process is a strong solution of the stochastic differential equation (1) with drift coefficient , diffusion coefficient and initial value , if for every 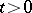with probability one:

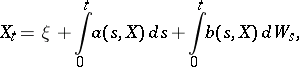(2)

where it is supposed that the integrals in (2) are defined.

The first general result on the existence and uniqueness of a strong solution of a stochastic differential equation of the form

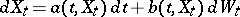(3)

was obtained by K. Itô. He demonstrated that if for every 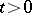the functions 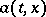and satisfy a Lipschitz condition with respect to and increase not faster than linearly, then a continuous solution 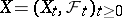of the equation (3) exists, and this solution is unique in the sense that if is another continuous solution, then

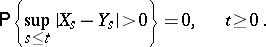If , the measurability and boundedness of the drift coefficient (vector) guarantees the existence and uniqueness of a strong solution of (3). The equation , generally speaking, does not have a strong solution for any bounded non-anticipative functional .

When studying the concept of a weak solution of the stochastic differential equation (1), the probability space 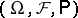with the family of 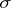-algebras , the Wiener process and the random variable 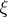are not fixed in advance, but the non-anticipative functionals 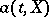, , 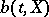defined for continuous functions , and the distribution function 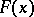(so to speak, the initial value) are fixed. Then by a weak solution of the equation (1) with given , and 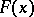one understands a set of objects

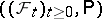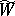where is a Wiener process relative to , and and 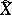are related by

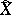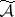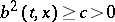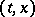and . The term "weak solution" sometimes applies only to the process that appears in the set . A weak solution of equation (3) exists under weaker hypotheses. It is sufficient, for example, that , and that be continuous in , that 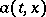be measurable in 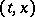, and that .

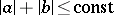The development of the theory of stochastic integration (see Stochastic integral) using semi-martingales (cf. Semi-martingale) and random measures has led to the study of more general stochastic differential equations, where semi-martingales and random measures are used as generators (along with a Wiener process). The following result is typical. Let be a probability space, let 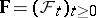be an increasing family of 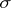-algebras, let 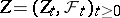be an 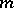-dimensional semi-martingale, and let be a matrix consisting of non-anticipative functionals 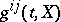such that

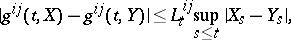where the 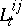do not increase too rapidly (in 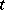). Then the stochastic differential equation , , 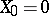has a unique strong solution.

If the functions 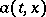and 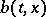, , 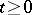, 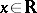satisfy a Lipschitz condition (in ) and do not increase faster than linearly, then the solution 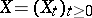of equation (3) (unique up to stochastic equivalence) will be a Markov process. If, moreover, 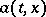and 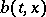are continuous in all variables, then this will be a diffusion process. Using stochastic differential equations, starting only from a Wiener process, it is thus possible to construct Markov and diffusion processes.

Given certain extra conditions of smoothness on the functions 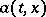and 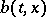, the solution of equation (3) with initial condition 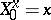is such that the function , given a sufficiently smooth function 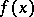, satisfies the backward Kolmogorov equation

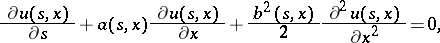in the domain 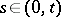, , with the boundary condition

References

[1]	I.I. Gikhman, A.V. Skorokhod, "Stochastic differential equations and their applications" , Springer (1972) (Translated from Russian)
[2]	R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1–2 , Springer (1977–1978) (Translated from Russian)

References

[a1]	L. Arnold, "Stochastic differential equations" , Wiley (1974) (Translated from Russian)
[a2]	H. Bunke, "Gewöhnliche Differentialgleichungen mit zufällige Parametern" , Akademie Verlag (1972)
[a3]	A. Freedman, "Stochastic differential equations and applications" , 1 , Acad. Press (1975)
[a4]	R.Z. [R.Z. Khasmins'kii] Hasminski, "Stochastic stability of differential equations" , Sijthoff & Noordhoff (1980) (Translated from Russian)
[a5]	N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland & Kodansha (1981)
[a6]	T.T. Soong, "Random differential equations in science and engineering" , Acad. Press (1973)
[a7]	S.K. Srinivasan, R. Vasudevan, "Introduction to random differential equations and their applications" , Amer. Elsevier (1971)
[a8]	R.L. Stratonovich, "Topics in the theory of random noise" , 1–2 , Gordon & Breach (1963–1967)
[a9]	D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979)
[a10]	Th. Gard, "Introduction to stochastic differential equations" , M. Dekker (1988)
[a11]	B. Øksendahl, "Stochastic differential equations" , Springer (1987)
[a12]	P. Protter, "Stochastic integration and differential equations" , Springer (1990)
[a13]	S. Albeverio, M. Röckner, "Stochastic differential equations in infinite dimensions: solutions via Dirichlet forms" Probab. Th. Rel. Fields , 89 (1991) pp. 347–386
[a14]	K.D. Elworthy, "Stochastic differential equations on manifolds" , Cambridge Univ. Press (1982)
[a15]	M. Emery, "Stochastic calculus in manifolds" , Springer (1989) ((Appendix by P.A. Meyer.))
[a16]	K. Sobczyk, "Stochastic differential equations. With applications to physics and engineering" , Kluwer (1991)