Euclidean ring
From Encyclopedia of Mathematics
An integral domain with an identity such that to each non-zero element 
of it corresponds a non-negative integer 
satisfying the following requirement: For any two elements 
and 
with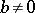 
one can find elements 
and 
such that
 |
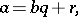where eithe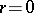r 
or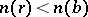 
.
Every Euclidean ring is a principal ideal ring and hence a factorial ring; however, there exist principal ideal rings that are not Euclidean. Euclidean rings include the ring of integers (the absolute value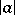 
plays the part of 
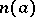), and also the ring of polynomials in one variable over a field (
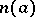is the degree of the polynomial). In any Euclidean ring the Euclidean algorithm can be used to find the greatest common divisor of two elements.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
How to Cite This Entry:
Euclidean ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_ring&oldid=18798
Euclidean ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_ring&oldid=18798
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article