Character of a C*-algebra
A non-zero lower semi-continuous semi-finite trace  on a
on a  -algebra
-algebra  satisfying the following condition (cf. Trace on a
satisfying the following condition (cf. Trace on a  -algebra): If
-algebra): If  is a lower semi-continuous semi-finite trace on
is a lower semi-continuous semi-finite trace on  and if
and if  for all
for all  , then
, then 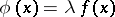 for a certain non-negative number
for a certain non-negative number 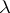 and all elements
and all elements  in the closure of the ideal
in the closure of the ideal 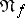 generated by the set
generated by the set  . There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of
. There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of  admitting a trace and the set of characters of
admitting a trace and the set of characters of 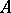 defined up to a positive multiplier (cf. Factor representation); this correspondence is established by the formula
defined up to a positive multiplier (cf. Factor representation); this correspondence is established by the formula 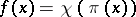 ,
,  , where
, where 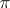 is the factor representation of
is the factor representation of  admitting the trace
admitting the trace 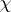 . If the trace
. If the trace 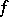 on
on  is finite, then the character is said to be finite; a finite character is continuous. There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of finite type of a
is finite, then the character is said to be finite; a finite character is continuous. There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of finite type of a  -algebra
-algebra  and the set of finite characters of
and the set of finite characters of 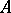 with norm 1. If
with norm 1. If  is commutative, then any character of the commutative algebra
is commutative, then any character of the commutative algebra  is a character of the
is a character of the  -algebra
-algebra 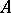 . If
. If  is the group
is the group  -algebra of a compact group
-algebra of a compact group 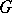 , then the characters of the
, then the characters of the 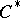 -algebra
-algebra  are finite, and to such a character with norm 1 there corresponds a normalized character of
are finite, and to such a character with norm 1 there corresponds a normalized character of 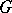 .
.
References
| [1] | J. Dixmier, "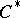 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Character of a C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_a_C*-algebra&oldid=18796